What Is 2 5/8 as a Decimal + Solution With Free Steps
The fraction 2 5/8 as a decimal is equal to 2.625.
When a whole number and a proper fraction are expressed together, a mixed fraction is produced. For instance, combining a whole number 2 plus the proper fraction 5/8 results in the mixed fraction 21/8. A mixed fraction is typically employed to represent a number that lies between two whole integers.
These fractions are frequently converted into decimal numbers with a fractional component and a whole number part separated by a decimal point because decimal numbers are easier to employ in mathematical computations than fractions. There are many options for doing this.
One method for converting 2 5/8 to its decimal number is the Long Division method, which is explained in greater detail below.
Solution
A mixed fraction must first be transformed into an improper fraction to be solved. To do this, we add the numerator, 5, by the product of the denominator, 8, and the whole number, 2.
The value we obtain as a result is the improper fraction’s numerator, and its denominator will be the same as that of the mixed fraction. As a result, we must solve the improper fraction 21/8.
Here, the numerator 21 is the Dividend and the denominator 8 is the Divisor.
Dividend = 21
Divisor = 8
The result of the fraction in decimal form is known as the Quotient.
Quotient = Dividend $\div$ Divisor = 21 $\div$ 8
Solution by long division method is: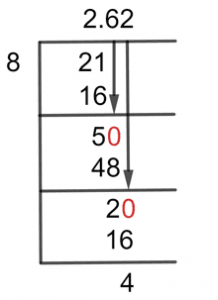
Figure 1
21/8 Long Division Method
Given a fraction’s step-by-step solution is:
21 $\div$ 8
The remainder is a division-specific term that is used to describe the remaining number after the incomplete division.
Here we have a numerator of 21 greater than a denominator of 8, so we can divide them as follows:
21 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
The generated Remainder after this division is 21 – 16 = 5.
The Decimal point must now be added to the quotient because the solution cannot be completed without it. As a result, we can now multiply our Remainder by 10.
So the Remainder now we have is 50.
50 $\div$ 8 $\approx$ 6
Where:
8 x 6 = 48
So, after this step, the Remainder is equal to 2. Bringing in another zero to its right will give 20, and will not add a decimal point to the quotient because it was already added in the previous step.
20 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
So we have a resulting Quotient equal to 2.62 with a Remainder of 4 for the given mixed fraction of 2 5/8. This suggests that if we keep solving, we might be able to get a more accurate answer.
Images/mathematical drawings are created with GeoGebra.
