What is 2 1/8 as a Decimal + Solution With Free Steps
The fraction 2 1/8 as a decimal is equal to 2.125.
The fraction 2 1/8 is a mixed fraction in which 2 is a whole number and 1/8 is a proper fraction. For converting 2 1/8 into a decimal form, this mixed fraction first needs to be converted into an improper function.
In an improper function, the numerator is greater than the denominator. Similarly, in a proper fraction, the numerator is less than the denominator.
The conversion of 2 1/8 into a decimal form is carried out by the Long Division Method. Although division can appear to be a lengthy and tricky concept, but yet there is a simple solution. Let’s dive right into this Long Division solution.
Solution
To begin with the long division method, first convert the mixed fraction into an improper fraction. This can be done by multiplying the denominator with the whole number part of the mixed fraction and then adding in the numerator.
So in this way solving the 2 1/8 mixed fraction gives 17/8 as the improper function. Let’s first revise the terms which are associated with the division before beginning the division itself.
The term “Dividend” is used for the numerator of the fraction and the term “Divisor” is used for the denominator of the fraction. So the dividend and divisor from 17/8 are given below:
Dividend = 17
Divisor = 8
The result obtained upon the division of the dividend with the divisor is known as the “Quotient” and the leftover numbers are referred to as the “Remainder.”
Dividend $\div$ Divisor = Quotient
The division process usually comes to an end when the remainder is zero.
The long division of 17/8 is given below:
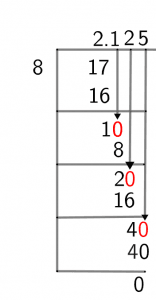
Figure 1
2 1/8 by Long Division
The long division of 2 1/8 can be carried out by first simplifying the mixed fraction. The result is 17/8 and its long division is given below:
17 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
Since the remainder obtained after this first step of division is 1, which is less than the divisor, hence we will now insert a decimal point to multiply the dividend by 10. After adding the decimal point, the dividend becomes 10. The division is shown below:
10 $\div$ 8 $\approx$ 1
Where:
1 x 8 = 8
Again, the remainder is 2 which is less than the divisor. So repeating the process of multiplying the dividend by 10 gives 20 as the result. The division is shown below:
20 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
Now the remainder obtained is 4, which is less than the divisor so repeating the process of multiplication with the dividend again gives 40. The division is shown below:
40 $\div$ 8 = 5
The remainder obtained now is zero, which indicates the end of the division. Hence, the division of 2 1/8 gives 2.125 as the quotient.
All images/mathematical drawings are created with GeoGebra.
