What Is 1/11 as a Decimal + Solution With Free Steps
The fraction 1/11 as a decimal is equal to 0.0909090909.Fractions are written in p/q form and have a numerator and a denominator. The numerator and denominator are shown by the letters p and q, respectively. To make fractions easier to understand, we convert them to decimal values, and this conversion calls for the mathematical operation known as division.Among all the mathematical operations, the division seems the most challenging, but it is not. Using a technique known as the Long Division approach, we can convert fractions to their decimal equivalent.We can apply the long division method to the provided fraction of 1/11 to determine its decimal value.
Solution
Understanding keywords is necessary before using the long division approach to discover the answer. “Dividend” and “divisor” are key terms. The fraction’s denominator is referred to as the divisor, while its numerator is known as the dividend. When discussing the p/q form, the p in the fraction is known as the dividend and the q as the divisor.
The dividend and the divisor are as follows for the given fraction of 1/11:
Dividend = 1
Divisor = 11
Understanding the concept of Quotient is also important. After applying the long division method, it is essentially the result of the fraction in the decimal value.
Quotient = Dividend $ \div $ Divisor = 1 $ \div $ 11
The long division method is as under for the given fraction of 1/11: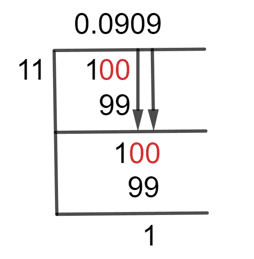
Figure 1
1/11 Long Division Method
We have:
1 $ \div $ 11
Here, the fraction has a numerator of 1 and a denominator of 11. It is obvious that, because the numerator is less than the denominator, we cannot divide these integers directly. To get to our solution, we must therefore add zero to the dividend’s right side. The decimal point must be added to the quotient to achieve that.
The Remainder is the number that remains when two numbers cannot be divided evenly by one another. So by adding zero, we have a remainder of 10, but still less than the divisor, so we will add another zero to its right side. To add two consecutive zeros, we will also add one zero in the quotient. So now we have a reminder of 100.
100 $ \div $ 11 $ \approx $ 9
Where:
11 x 9 = 99
The remainder we get after this step is 1. So we will add zero to its right and it becomes 1. So here is the case again of the remainder being less than the divisor even by adding zero to its right. So we will repeat the same step as we did in the previous step. Again, now we have the remainder of 100.
100 $ \div $ 11 $ \approx $ 9
Where:
11 x 9 = 99
So we have a Remainder of 1 after this step and a resulting Quotient of 0.0909 for the given fraction of 1/11.