
To solve this question, we have to determine the point on the hyperbola xy = 8 that is closest to the point (3,0).
A hyperbola is defined as a conic section that is produced by the intersection of a plane and circular cone at any given angle so that halves of the circular cone are bisected. This bisection generates two similar curves that are exact mirror images of each other called Hyperbola.
Here are some important terms associated with the construction of a hyperbola:
- Center of Hyperbola O
- Foci of Hyperbola F and $F^{’}$
- Major axis
- Minor axis
- Vertices
- Eccentricity (e>1), defined as e = c/a where c, is the distance from the focus and $a$ is the distance from the vertices.
- Transverse axis
- Conjugate axis
The standard equation of the hyperbola is given as:
\[ \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1\]
Another standard equation for the hyperbola is given as:
\[ \dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1\]
Expert Solution:
The equation for the hyperbola is given as:
\[ xy= 8 \]
Modifying the equation gives us:
\[ y = \dfrac{8}{x} \]
So, any point on the given hyperbola can be defined as:
\[ (x, y) = \bigg( x, \dfrac{8}{x}\bigg) \]
Now, let’s find the distance of $ \bigg(x, \dfrac{8}{x} \bigg)$ from the given point $(3,0)$ on the hyperbola.
The formula for calculating distance is given as:
\[ distance = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \]
The two points are:
$(x_1, y_1)$ = $(3, 0)$
$(x_2, y_2)$ = $\bigg(x, \dfrac{8}{x}\bigg)$
The distance is given as:
\[ d = \sqrt {(x – 3)^2 + \bigg(\dfrac{8}{x} – 0 \bigg)^2} \]
\[ d = \sqrt{(x^2 – 6x + 9) + \bigg(\dfrac{64}{x^2}\bigg)} \]
Numerical Results:
To calculate the minimum distance, let’s take the derivative of the distance $d$ with respect to $x$ and equate it to zero.
\[ d = \sqrt {(x^2 – 6x + 9) + \bigg(\dfrac{64}{x^2}\bigg)} \]
Squaring on both sides:
\[ d^2 = x^2 – 6x + 9 + \dfrac{64}{x^2} \]
Taking derivative on both sides w.r.t $x$:
\[ \dfrac{d(d^2)}{dx} = \dfrac{d(x^2)}{dx} – \dfrac{6d(x)}{dx} + \dfrac{d(9)}{dx} + \dfrac{64d(x^{-2})}{dx} \]
\[ 2dd’ = 2x – 6 + 0 – \dfrac{128}{x^3} \]
\[ 2dd’ = x – 3+ 0 – \dfrac{64}{x^3} \]
Equating the equation to zero:
\[ 0 = x – 3 – \dfrac{64}{x^3} \]
\[ x^4 – 3x^3 – 64 = 0 \]
Solving the above equation gives us:
\[ x = 4 \]
\[ x = -2.949 \]
Considering $x=4$ as putting $x=4$ makes the equation $x^4 – 3x^3 – 64$ equivalent to $0$.
So, the point is given as:
\[ \bigg(x, \dfrac{8}{x}\bigg) = \bigg(4, \dfrac{8}{4}\bigg) \]
\[ \bigg(x, \dfrac{8}{x}\bigg) = (4,2) \]
Hence, $(4,2)$ is the point on hyperbola that is closest to $(3,0)$.
It can also be represented graphically by using the equation:
\[ d’ = f’(x) = x^4 -3x^3 – 64 \]
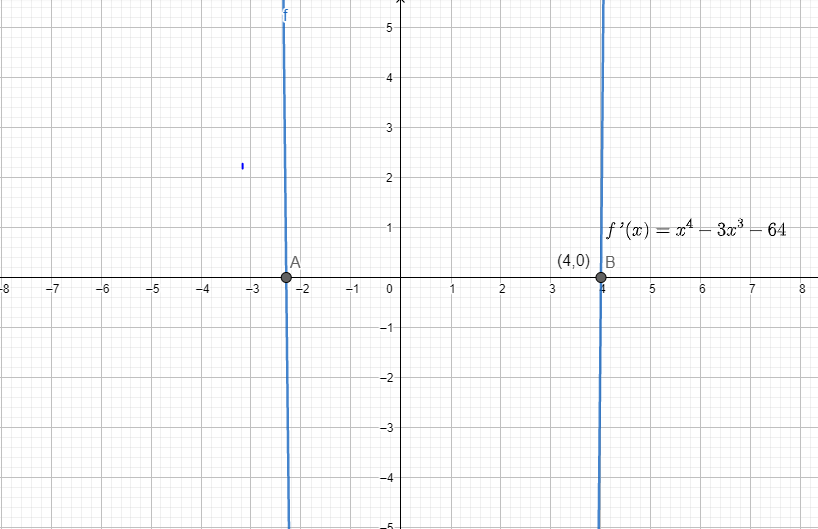
$Figure 1$
Therefore, the graph is shown in $Figure 1$ and indicates that local minima occur at $(4,0).
So the closest point to $(3,0)$ is $(4,2)$.
Example:
Find the point on the hyperbola $xy= -8$ that is closest to the point $(-3,0)$.
The equation for hyperbola is given as:
\[ xy = -8 \]
\[ y = \dfrac{-8}{x} \]
Using the distance formula to calculate the distance,
\[ distance = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \]
\[ distance = \sqrt{(x + 3)^2 + \bigg(\dfrac{-8}{x} – 0\bigg)^2} \]
\[ distance = \sqrt{(x^2 + 6x + 9 ) + \bigg(\dfrac{64}{x^2}\bigg)} \]
Squaring both sides gives us:
\[ d^2 = x^2 + 6x + 9 + \dfrac{64}{x^2} \]
Taking derivative w.r.t $x$:
\[ 2dd’ = 2x + 6 – \dfrac{128}{x^3} \]
Equating the above equation to zero for calculating the minimum distance gives us:
\[ x^4 + 3x^3 – 64 = 0 \]
Solving the equation:
\[ x = -4 \]
\[ x = 2.29\]
Considering $x=4$ as putting $x=4$ makes the equation $x^4 – 3x^3 – 64$ equivalent to $0$.
\[ \bigg(x, \dfrac{8}{x}\bigg) = (-4, -2) \]
It can be represented graphically as:
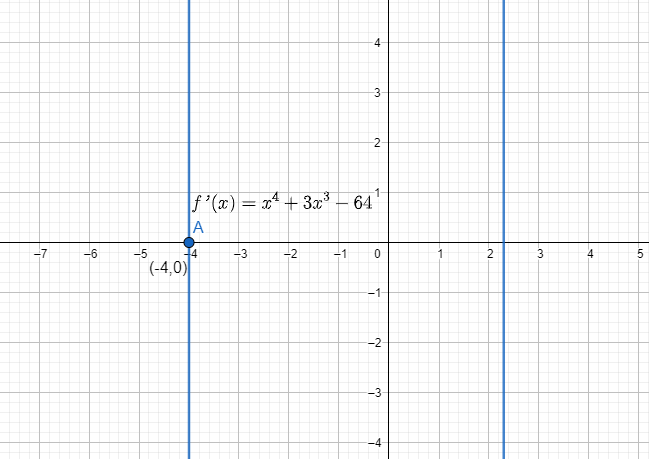
$Figure 2$
Hence, the graph in $Figure 2$ shows us that local minima occur at $(-4,0).
Therefore, the point closest to $(3,0)$ is $(-4, -2)$.
Images/Mathematical drawings are created using Geogebra.
