
If the axis is passing through mass A in the direction perpendicular to the page, calculate its moment of inertia with the proper unit and up to two significant figures.
If the axis is passing through masses B and C, calculate its moment of inertia with the proper unit and up to two significant figures.
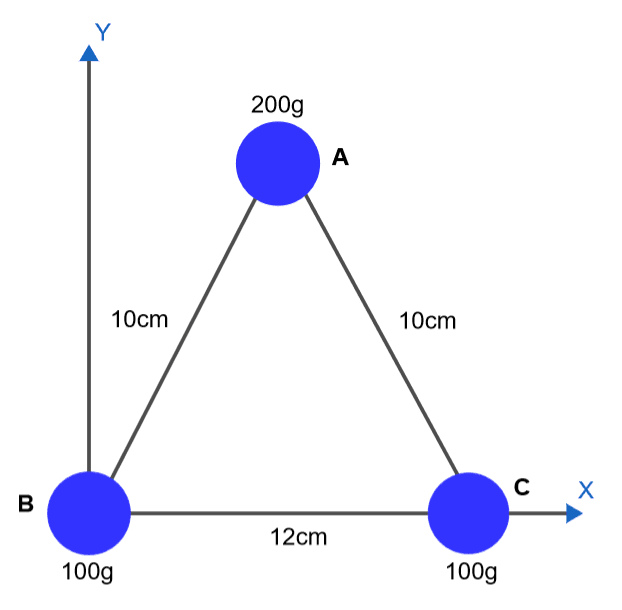
Figure 1
The aim of this question is to find the Moment of Inertia about the required axes.
The basic concept behind this article is the Moment of Inertia or Rotational Inertia, which is represented by the symbol $I$. It is defined as the characteristic of a rotating body due to which it opposes the acceleration in the angular direction. It is always represented in relation to an axis of rotation. The Moment of Inertia is represented by an SI unit of $kgm^2$ and expressed as follows:
\[I\ =\ m\ \times\ r^2\]
where,
$I=$ Moment of Inertia
$m=$ Sum of the product of the mass
$r=$ Distance from the axis of the rotation
Expert Answer
Given that:
Mass $A=200g=m_1$
Mass $B=100g=m_2$
Mass $C=100g=m_3$
Distance between Mass $A\ and\ B\ =\ 10cm$
Distance between Mass $A\ and\ C\ =\ 10cm$
Distance between Mass $B\ and\ C\ =\ 12cm$
Part-A
Axis is passing perpendicularly through Mass $A$, hence we will calculate the moment of inertia of the system by considering Mass $B$ and Mass $C$ which are lying at a distance of $10cm$ from Mass $A$. As per the expression for Moment of Inertia, we will consider the moment created by both Masses $B$ and $C$ around the axis passing through Mass $A$ as follows:
\[I_A=m_2{r_2}^2+m_3{r_3}^2\]
Substituting the values:
\[I_A=[100g\times{(10cm)}^2]+[100g×(10cm)2]\]
\[I_A=10000g{\rm cm}^2+10000g{\rm cm}^2\]
\[I=20000g{\rm cm}^2\]
\[I_A=20000\ \frac{kg}{1000}\left(\frac{m}{100}\right)^2\]
\[I_A=2.0\ \times{10}^{-3}kgm^2\]
Part-B
The axis of rotation is passing through Masses B and C.
If we consider the placement of masses in the form of a triangle, the distance $r$ from Mass $A$ to the axis of rotation will be the height of the triangle, and the base will be half of the distance between Mass $B$ and $C$.
Hence as per Pythagoras’ Theorem:
\[{\rm Hypotenuse}^2={\rm Base}^2+{\rm Height}^2\]
\[{10}^2=\left(\frac{12}{2}\right)^2+r^2\]
\[r=\sqrt{{10}^2-6^2}\]
\[r=\sqrt{64}\]
\[r=8cm\]
As per the expression for Moment of Inertia, we will consider the moment created by Mass $A$ around the axis passing through Masses $B$ and $C$ as follows:
\[I_{BC}=m_1r^2\]
\[I_{BC}=200g\ \times{(8cm)}^2\]
\[I_{BC}=200g\ \times{64cm}^2\]
\[I_{BC}=200g\ \times{64cm}^2\]
\[I_{BC}=12800\times\frac{kg}{1000}\left(\frac{m}{100}\right)^2\]
\[I_{BC}=1.28\times{10}^4\times{10}^{-3}\times{10}^{-4}\ kgm^2\]
\[I_{BC}=1.28\times{10}^{-3}\ kgm^2\]
Numerical Result
Part-A. If the axis is passing through Mass $A$ in the direction perpendicular to the page, its moment of inertia is:
\[I_A=2.0\ \times{10}^{-3}kgm^2\]
Part-B. If the axis is passing through Masses $B$ and $C$, its moment of inertia is:
\[I_{BC}=1.28\times{10}^{-3}\ kgm^2\]
Example
A Car having a mass of $1200kg$ is taking a turn around a roundabout having a radius of $12m$. Calculate the moment of inertia of the car around its roundabout.
Given that:
Mass of the Car $m=1200kg$
The radius of the turn $r=12m$
As per the expression for Moment of Inertia:
\[I\ =\ m\ \times\ r^2\]
\[I\ =\ 1200kg\ \times\ {(12m)}^2\]
\[I\ =\ 172800kgm^2\]
\[Moment\ of\ Inertia\ I\ =\ 1.728\times{10}^5\ kgm^2\]
Image/Mathematical drawings are created in Geogebra.
