Factors of 576: Prime Factorization, Methods, Tree, and Examples

Factors are numbers or mathematical expressions, that when undergoing division, divide the number completely, without leaving any remainder behind. In other words, the factors of a given number are also referred to as its divisors.  

Figure 1 – All Factors of 576

Factors of a specific number can be both positive and negative integers that when multiplied in pairs, resulting in producing another natural or whole number. 

The current article focuses on paying special attention to the methods and techniques used to calculate the factors of the number 576, its prime factorization, factor tree, and factor pairs.

What Are the Factors of 576?

The factors of number 576 are the following: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, and 576.  

All the above-mentioned numbers are recognized as the factors of number 576 as these are the natural numbers that when divided by the number 576, result in producing zero as the remainder.  

Due to its nature as an even and composite number, 576 has factors besides just itself and the number 1. In simple words, the total number of factors of number 576 is 21, as stated above. 

How To Calculate the Factors of 576?

You can calculate the factors of 576 using the division or multiplication method.

By multiplying two numbers in pairs, you can determine the factors of the number 576, further ensuring that the result of the multiplication is 576.

The following is the list of pair multiplication for the number 576:

1 x 576 = 576 

OR

576 x 1 = 576 

Similarly,

2 x 288 = 576 

3 x 192 = 576 

4 x 144 = 576 

6 x 96 = 576 

8 x 72 = 576 

9 x 64 = 576 

12 x 48 = 576 

16 x 36 = 576 

18 x 32 = 576 

24 x 24 = 576 

Hence, it has been seen that the numbers 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576 are the factors of 576. 

Similarly, another method to calculate factors of 576 is the division method. According to this method, if the suggested number gets divided by 576 and the division leaves no or zero remainder behind then, the number proposed is going to be recognized as the factor of 576.  

The following steps are to be adopted to calculate the factors of 576.

At first, divide the smallest number i.e. 1 with the given number 576. Check for the remainder. Is the remainder zero?

\[ \dfrac {576}{1} = 576,r=0 \]

Yes, the remainder is zero. Hence, it is proved that the number 1 is a factor of 576.

The number 1 is also known as the universal factor, as every number is divisible by 1. 

Now, divide 576 by the number 2 such that,

\[ \dfrac {576}{2} = 288,r=0 \]

As the remainder of the above division is zero, therefore, 2 is also a factor of 576.

Keep on dividing 576 by the other set of numbers using the same method, as described previously. 

\[ \dfrac {576}{3} = 192 \]

\[ \dfrac {576}{4} = 144 \]

\[ \dfrac {576}{6} = 96 \]

\[ \dfrac {576}{8} = 72 \]

\[ \dfrac {576}{9} = 64 \]

\[ \dfrac {576}{12} = 48 \]

\[ \dfrac {576}{16} = 36 \]

\[ \dfrac {576}{18} = 32 \]

\[ \dfrac {576}{24} = 24 \]

Hence, it has been seen that the numbers 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, and 576 are the recognized factors of 576. 

As mentioned previously, each number has both positive and negative factors, and the negative factors of any number are the additive inverse of its positive factors. 

Following is the list of the negative factors of 576.

Negative Factors of 576 =  -1, -2, -3, -4, -6, -8, -9, -12, -16, -18, -24, -32, -36, -48, -64, -72, -96, -144, -192, -288, -576

Similarly, the list of the positive factors of 576 is given below.

Positive Factors of 576 = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576

Factors of 576 by Prime Factorization

Prime Factorization is defined as the technique that focuses on breaking a well-defined number into its prime factors till the end product received is 1. 

Prime factors are those integers or numbers that can only be divided evenly by themselves and by the number 1. Because 0 and 1 are not clearly defined prime numbers, any number that satisfies the requirements listed in the definition of prime factors can be the prime factor of a given integer; however, it can never be 0 or 1.

The prime factorization of 576 is given as, 

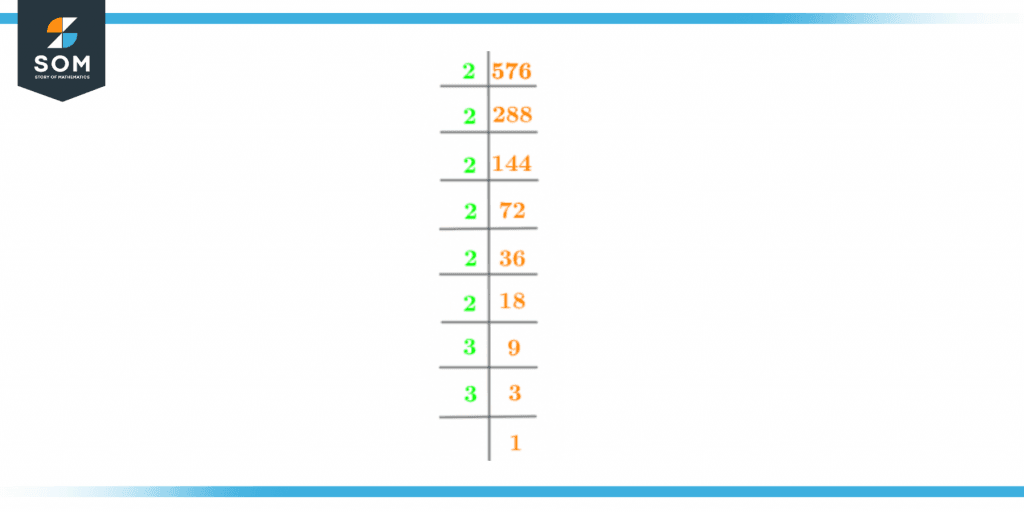
Figure 2 – Prime factorization of 576

Also, the prime factorization of 576 can be expressed as the following expression,

$2^{6}$ x $3^{2}$ = 576 

Hence, there are 8 prime factors of 576. 

The prime factors of 576 are: 2,2,2,2,2,2,3,3

Factor Tree of 576

A factor tree is the geometric representation of the prime factors of a number.  

The following image shows the factor tree of the number 576,

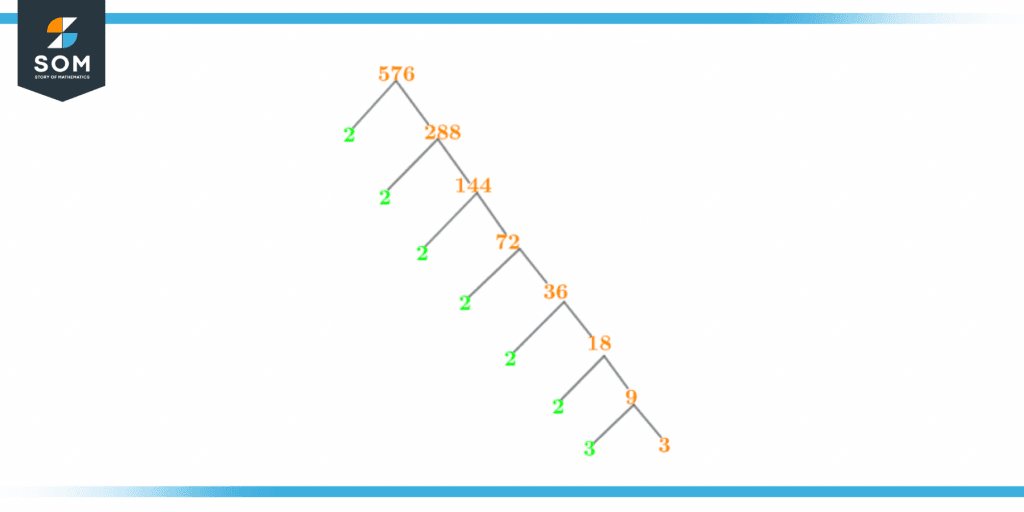
Figure 3 – Factor Tree of 576

Factors of 576 in Pairs

Factor pairs are those groups of numbers that, when multiplied together, provide the same result as the product of which they are a factor. The pair of factors can be both a set of negative or positive integers. 

The method to find the pair of factors for 576 is similar to the technique applied to calculate the factor pairs of any other number. Hence, the pair of factors of the number 576 are given as,

1 x 576 = 576 

Where, (1, 576) is a factor pair of 576.

Similarly, 

2 x 288 = 576 

3 x 192 = 576 

4 x 144 = 576 

6 x 96 = 576 

8 x 72 = 576 

9 x 64 = 576 

12 x 48 = 576 

16 x 36 = 576 

18 x 32 = 576 

24 x 24 = 576 

Where, (2, 288), (3, 192), (4, 144), (6, 96), (8, 72), (9, 64), (12, 48), (16, 36), (18, 32), and (24, 24) are the factor pairs of 576.

Factors of 576 Solved Examples

Now, let us solve a few examples to test our understanding of the above article.

Example 1

Charles wanted to find the H.C.F of 576 for his mathematics assignment. How will Charles find the correct answer from the well-defined list of factors of 576?

Solution

Given that,

Factors of 576 =  1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576

From the list, it is clear that the H.C.F of factors of 576 is 576 itself. 

Example 2

Windy wants to write the prime factors of 576. Can you help her?

Solution

Given that, 

The prime factorization of 576 is expressed as, $2^{6}$ x $3^{2}$ = 576 

Therefore, the prime factors of 576 are 2,2,2,2,2,2,3,3.

Images/mathematical drawings are created with GeoGebra.