Exterior Angle Theorem – Explanation & Examples

So, we all know that a triangle is a 3-sided figure with three interior angles. But there exist other angles outside the triangle, which we call exterior angles.

We know that the sum of all three interior angles is always equal to 180 degrees in a triangle.

Similarly, this property holds for exterior angles as well. Also, each interior angle of a triangle is more than zero degrees but less than 180 degrees. The same goes for exterior angles.

In this article, we will learn about:

• Triangle exterior angle theorem,
• exterior angles of a triangle, and,
• how to find the unknown exterior angle of a triangle.

What is the Exterior Angle of a Triangle?

The exterior angle of a triangle is the angle formed between one side of a triangle and the extension of its adjacent side.

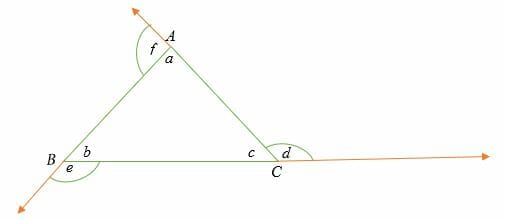
In the illustration above, the triangle ABC’s interior angles are a, b, c, and the exterior angles are d, e, and f. Adjacent interior and exterior angles are supplementary angles.

In other words, the sum of each interior angle and its adjacent exterior angle is equal to 180 degrees (straight line).

Triangle Exterior Angle Theorem

The exterior angle theorem states that the measure of each exterior angle of a triangle is equal to the sum of the opposite and non-adjacent interior angles.

Remember that the two non-adjacent interior angles opposite the exterior angle are sometimes referred to as remote interior angles.

For example, in triangle ABC above;

⇒ d = b + a

⇒ e = a + c

⇒ f = b + c

Properties of exterior angles

• An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
• The sum of exterior angle and interior angle is equal to 180 degrees.

⇒ c + d = 180°

⇒ a + f = 180°

⇒ b + e = 180°

• All exterior angles of a triangle add up to 360°.

Proof: 

⇒ d + e + f = b + a + a + c + b + c

⇒ d +e + f = 2a + 2b + 2c

= 2(a + b + c)

But, according to triangle angle sum theorem,

a + b + c = 180 degrees

Therefore, ⇒ d +e + f = 2(180°)

= 360°

How to Find the Exterior Angles of a Triangle?

Rules to find the exterior angles of a triangle are pretty similar to the rules to find the interior angles. It is because wherever there is an exterior angle, there is an interior angle with it, and both add up to 180 degrees.

Let’s take a look at a few example problems.

Example 1

Given that for a triangle, the two interior angles 25° and (x + 15) ° are non-adjacent to an exterior angle (3x – 10) °, find the value of x.

Solution

Apply the triangle exterior angle theorem:

⇒ (3x − 10) = (25) + (x + 15)

⇒ (3x − 10) = (25) + (x +15)

⇒ 3x −10 = x + 40

⇒ 3x – 10 = x + 40

⇒ 3x = x + 50

⇒ 3x = x + 50

⇒ 2x = 50

x =25

Hence, x = 25°

Substitute the value of x into the three equations.

⇒ (3x − 10) = 3(25°) – 10°

= (75 – 10) ° = 65°

⇒ (x+15) = (25 + 15) ° = 40°

Therefore, the angles are 25°, 40° and 65°.

Example 2

Calculate values of x and y in the following triangle.

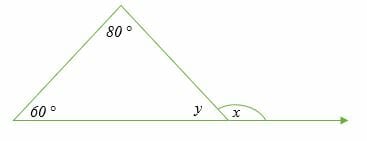
Solution

It is clear from the figure that y is an interior angle and x is an exterior angle.

By Triangle exterior angle theorem.

⇒ x = 60° + 80°

x = 140°

The sum of exterior angle and interior angle is equal to 180 degrees (property of exterior angles). So, we have;

⇒ y + x = 180°

⇒ 140° + y = 180°

subtract 140° from both sides.

⇒ y = 180° – 140°

y = 40°

Therefore, the values of x and y are 140° and 40°, respectively.

Example 3

The exterior angle of a triangle is 120°. Find the value of x if the opposite non-adjacent interior angles are (4x + 40) ° and 60°.

Solution

Exterior angle = sum of two opposite non-adjacent interior angles.

⇒120° =4x + 40 + 60

Simplify.

⇒ 120° = 4x + 100°

Subtract 120° from both sides.

⇒ 120° – 100° = 4x + 100° – 100°

⇒ 20° = 4x

Divide both sides by to get,

x = 5°

Therefore, the value of x is 5 degrees.

Verify the answer by substitution.

120°= 4x + 40 + 60

120° = 4° (5) + 40° + 60°

120° = 120° (RHS = LHS)

Example 4

Determine the value of x and y in the figure below.

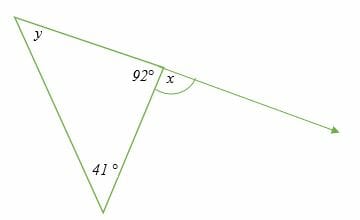
Solution

Sum of interior angles = 180 degrees

y + 41° + 92° = 180°

Simplify.

y + 133° = 180°

subtract 133° from both sides.

y = 180° – 133°

y = 47°

Apply the triangle exterior angle theorem.

x = 41° + 47°

x = 88°

Hence, the value of x and y is 88° and 47°, respectively.