
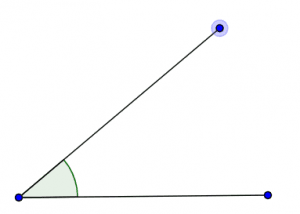
Figure (1): Angle given in the question statement
The aim of this question is to develop the ability to estimate angles to the nearest half radian just by visualizing them.
To estimate such angles, we need to imagine a circular scale of our choice in accordance with our required precision.
If we choose a circular grading of $ \dfrac{ 1 }{ 2 } \pi $ radians, then the scale looks something like the following figure (2):
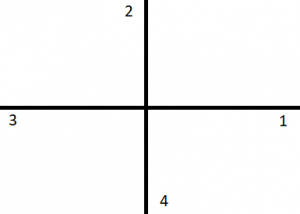
Figure (2): Angles with a circular grading of $ \dfrac{ 1 }{ 2 } \pi $ radians
Where 1, 2, 3 and 4 represent the angles $ \dfrac{ 1 }{ 2 } \pi, \ \pi, \ \dfrac{ 3 }{ 2 } \pi, \text{ and } 2 \pi $ radians, respectively.
Similarly, if we choose a circular grading of $ \dfrac{ 1 }{ 2 } \pi $ radians, then the scale looks something like the following figure (3):
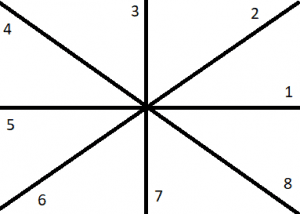
Figure (3): Angles with a circular grading of $ \dfrac{ 1 }{ 4 } \pi $ radians
Where 1, 2, 3, 4, 5, 6, 7, and 8 represent the angles $ \dfrac{ 1 }{ 4 } \pi, \ \dfrac{ 1 }{ 2 } \pi, \ \dfrac{ 3 }{ 4 } \pi, \pi, \dfrac{ 5 }{ 4 } \pi, \ \dfrac{ 3 }{ 2 } \pi, \ \dfrac{ 7 }{ 4 } \pi, \ \text{ and } 2 \pi $ radians, respectively.
In practice, we use the protractor scale to estimate the angles to the nearest degree in the lab or in the field. Since modern drawing applications use state-of-the-art computer software, such scales have very little use in the industry.
Expert Answer
Drawing the gird angles with a circular grading of $ \dfrac{ 1 }{ 4 } \pi $ radians on top of the given angle is drawn below in figure (4):
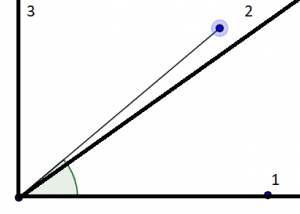
Figure (4): Given angle with a circular grading of $ \dfrac{ 1 }{ 4 } \pi $ radians
Now here we can easily visualize that the nearest half angle when the circular grading is $ \dfrac{ 1 }{ 4 } \pi $ radians can be approximated to the $ 2^{ nd } $ grading which is in-turn equal to the $ \dfrac{ 1 }{ 4 } \pi $ radians.
Numerical Result
\[ \text{ Estimated angle } \ = \ \dfrac{ 1 }{ 4 } \pi \ radians\]
Example
Estimate the nearest half angle of the following angle:
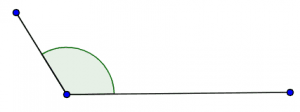
Figure (5): Angle given in the example statement
Drawing the gird angles with a circular grading of $ \dfrac{ 1 }{ 4 } \pi $ radians on top of the given angle is drawn below in figure (6):
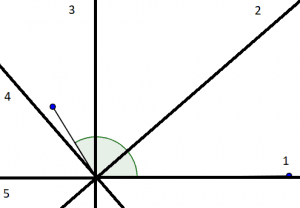
Figure (6): Given angle with a circular grading of $ \dfrac{ 1 }{ 4 } \pi $ radians
Now here we can easily visualize that the nearest half angle when the circular grading is $ \dfrac{ 1 }{ 4 } \pi $ radians can be approximated to the $ 4^{ th } $ grading which equals the $ \dfrac{ 3 }{ 4 } \pi $ radians.
Images/Mathematical drawings are created with Geogebra.
