Dividing Expressions – Methods & Examples

An algebraic expression is a mathematical phrase where variables and constants are combined using the operational (+, -, × & ÷) symbols. For example, 10x + 63 and 5x – 3 are examples of algebraic expressions.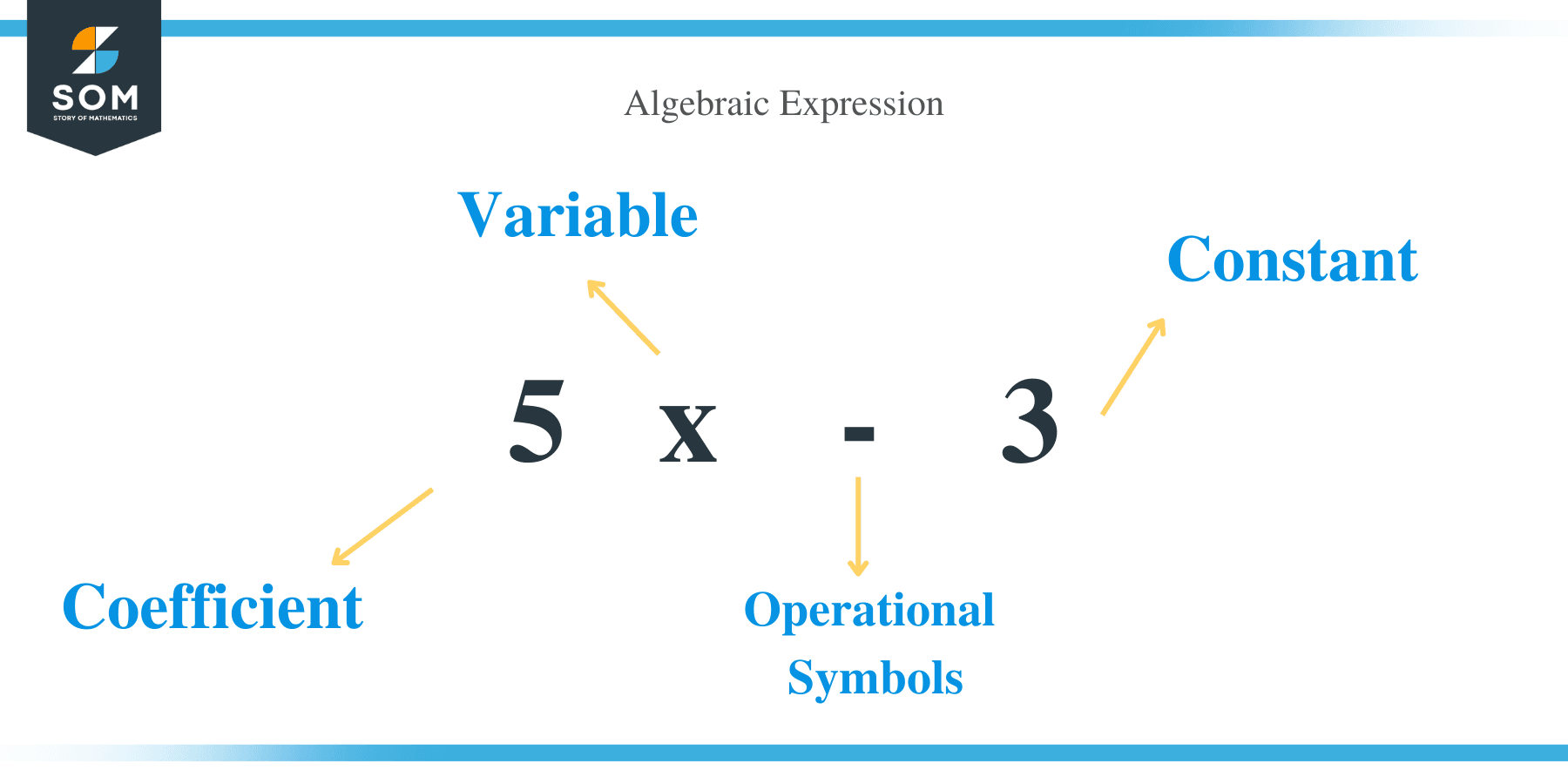

A rational expression is simply defined as a fraction in either or both the numerator and the denominator is an algebraic expression. Examples of rational fractions are: 3/ (x – 3), 2/ (x + 5), (4x – 1)/3, (x² + 7x)/6, (2x + 5)/ (x² + 3x – 10), (x + 3)/(x + 6) etc.

How to divide the ordinary fractions?

Rational expressions are divided by applying the same steps used to divide ordinary fractions having rational numbers. A rational number is a number that is expressed in the form of p/q, where ‘p’ and ‘q’ are integers and q ≠ 0. In other words, a rational number is simply a fraction where the integer a is the numerator, and integer b is the denominator.

Example of rational numbers include:
2/3, 5/8, -3/14, -11/-5, 7/-9, 7/-15 and -6/-11 etc.

Division of ordinary fractions is done by multiplying the first fraction by the reciprocal of the second fraction. For example, to divide, 4/3 ÷ 2/3, you find the product of the first fraction and the inverse of the second fraction; 4/3 x 3/2 = 2.

Other examples of dividing rational numbers are:

9/16 ÷ 5/8 = 9/16 × 8/5
= (9 × 8)/ (16 × 5) = 72/80
= 9/10
-6/25 ÷ 3/5 = -6/25 × 5/3
= {(-6) × 5}/(25 × 3)
= -30/75
= -2/5

How to Divide Rational Expressions?

Similarly, we invert or flip the second expression when dividing rational expressions and multiply it by the first expression.

Below is a summary of the steps followed when dividing rational expressions:

• Completely factor out the denominators and numerators of all expressions.
• Replace the division sign (÷) with the multiplication sign (x) and find the reciprocal of the second fraction.
• Reduce the fraction if possible.
• Now rewrite the remaining factor.

 

Example 1

Divide 4x/3 ÷ 7y/2

Solution

4x/3 ÷ 7y/2 = 4x/3 * 2/7y

=8x/21y

 

Example 2

Divide ((x + 3) / 2x²) ÷ (4 / 3x)

Solution

Change the division sign to multiplication sign and invert the second expression;

= (x + 3 / 2x²) × (3x/ 4)

Multiply the numerators and denominators separately if they cannot be factored out;

= [(x + 3) × 3x] / (2x² × 4)

= (3x² + 9x) / 8x²

Since there is a common factor of x in both the numerator and the denominator, therefore, this expression can be simplified as;

(3x² + 9x) / 8x² = x (3x+ 9) / 8x²

= (3x + 9) / 8x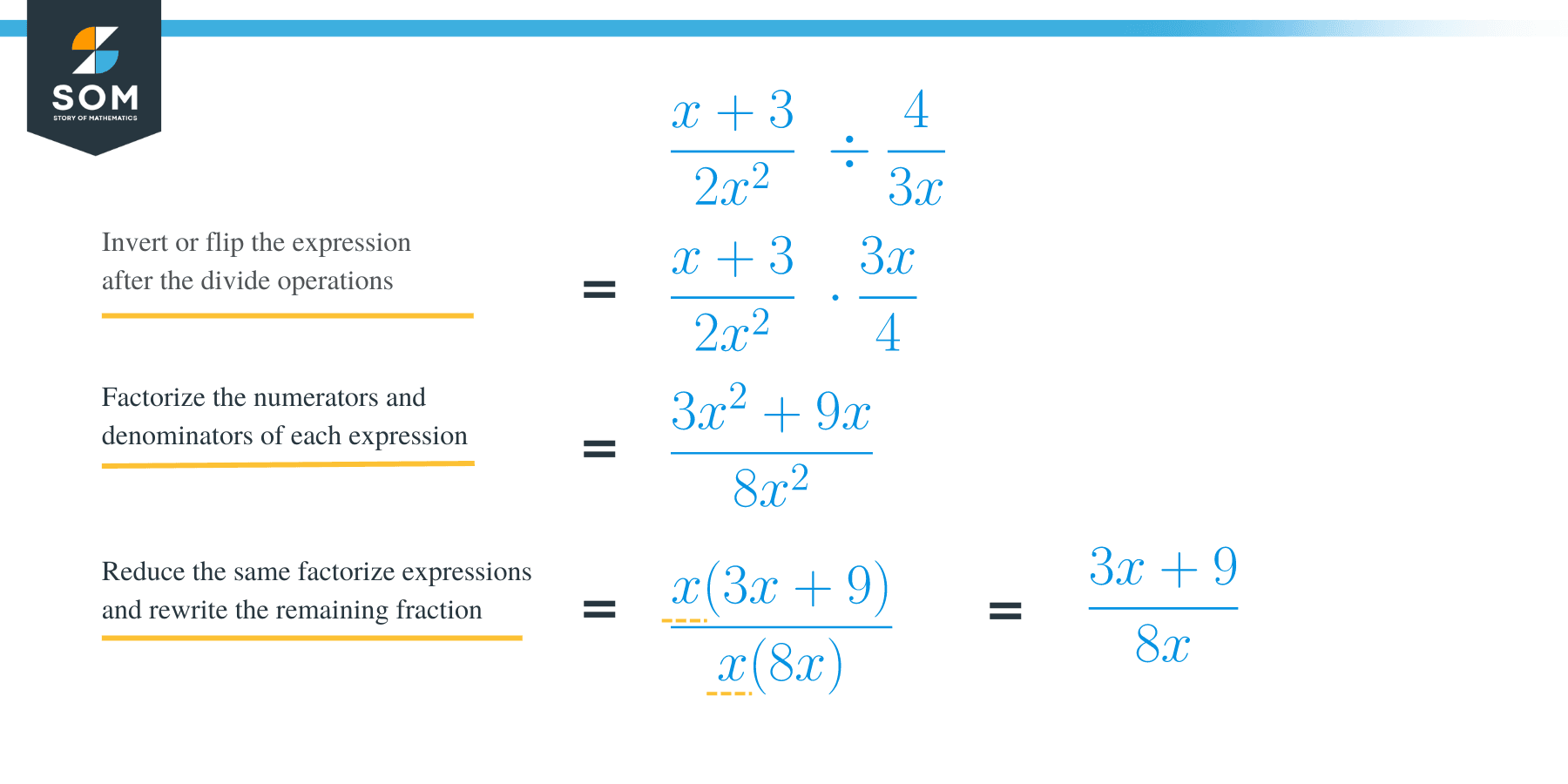

 

Example 3

Divide and then simplify.

(x ² − 4)/ (x + 6) ÷ (x + 2)/ (2x + 12)

Solution

Multiply the first expression by the reciprocal of the second expression;

The reciprocal of the second fraction (x + 2)/ (2x + 12x) is (2x + 12x)/ (x + 2)

(x ² − 4)/ (x + 6) ÷ (x + 2)/ (2x + 12) = (x ² − 4)/ (x + 6) * (2x + 12x)/(x + 2)

= Now multiply the numerators and the denominators.

= [(x² − 4) (2x + 12)]/ [(x + 6) (x + 2)]

Factor the terms in the numerator and cancel out the common factors

= [(x + 2) (x − 2) * 2(x + 6)]/ (x + 6) (x + 2)

Rewrite the remaining fraction;

=2(x − 2)/1= 2x−4

 

Example 4

Divide (x + 5) / (x – 4) ÷ (x + 1)/x

Solution

Find the reciprocal of the second expression;

Reciprocal of (x + 1)/x = x/x + 1

Now multiply the fractions;

= ((x + 5) * x) / ((x – 4) * (x + 1))

= (x² + 5x) / (x² – 4x + x – 4)

= (x² + 5x) / (x² – 3x – 4)

 

Example 5

Simplify {(12x – 4x ²)/ (x ² + x – 12)} ÷ {(x ² – 4x)/ (x ² + 2x – 8)}

Solution

Invert the second fraction and multiply;

= {(12x – 4x ²)/ (x ² + x – 12)} *{(x ² + 2x – 8)/ (x ² – 4x)}

Factor out both the both the numerators and denominators of each expression;

= {- 4x (x – 3)/(x-3) (x + 4)} * {(x – 2) (x + 4)/x (x + 2) (x – 2)}

Reduce or cancel the expressions and rewrite the remaining factors;

= -4/ x + 2

 

Practice Questions

Simplify the following rational expressions:

1. 2x/4y ÷ 3y/4xy²
2. (8x ² – 6x/ 4 – x) ÷ (4x ² -x – 3/ x ² -16) ÷ (2x + 8/-5x -5).
3. (x² – 7x + 10/ x ² – 9x + 14) ÷ (x ² + 6x + 5/ x ² – 6x -7)
4. (2x + 1/x² – 1) ÷ (2x ² + x/ x + 1)
5. (-3x ² +27/x³ – 1) ÷ (x – 3x/7x³ + 7x² + 7x) ÷ (21/x – 1)
6. (x² – 5x – 14/ x² – 3x + 2) ÷ (x² – 14x + 49/ x ² – 4)
7. When (4x + 55) is divided by (2x + 3), the result is 9. Find the value of x.

 

Answers

1. 2x²/3
2. 5x
3. x+2/x-2
4. 1/x (x – 1)
5. – x – 3
6. (x + 2)²/ (x – 1) (x – 7)
7. 2

Previous Lesson | Main Page | Next Lesson