- Home
- >
- Dividing Decimals – Explanation & Examples
JUMP TO TOPIC
Dividing Decimals – Explanation & Examples
 How to Divide Decimals?
How to Divide Decimals?
Working around decimal numbers seems to be a bit taxing whenever students are faced with the task of dividing decimals. Students spend most of their time figuring out how to solve problems involving division of decimals.
Decimal numbers provide a greater degree of accuracy when working with the numerical values of quantities. A long with this merit, the challenge of working with decimals numbers, which are more complex as compared to whole numbers, arises.
The purpose of this article is give an insight on how to take a step-by-step approach to the problem in hand and make division of decimals numbers as easy as possible. For this reason, problem solving involving the division of decimal numbers can be made easy by assuming the divisor is a whole number.
How to Divide Decimals by a Whole Number?
Division of a decimal number by a whole number is one the easiest operation of decimals. Before learning on how to carryout the division operation, let us review some of the terminologies used in this case:
- A dividend is the number to be divided. For example, in the division of the decimal number: 0.208 ÷ 65= 0.0032, the dividend is 0.208.
- The divisor is the number divided the dividend. In this example, the divisor is the number 65.
- This is the results after division.
- The remainder is a number left after division. There is no quotient in this example.
The following are the steps followed when performing this operation:
- When the dividend is a decimal number and the divisor is an integer, the decimal point in the dividend is ignored and treated as a whole number.
- by considering the dividend as a whole number, divide it by the divisor using regular long division method.
- Insert in the quotient the same number of decimal points as they are in the dividend
Let’s understand these steps by solving a few examples:
Example 1
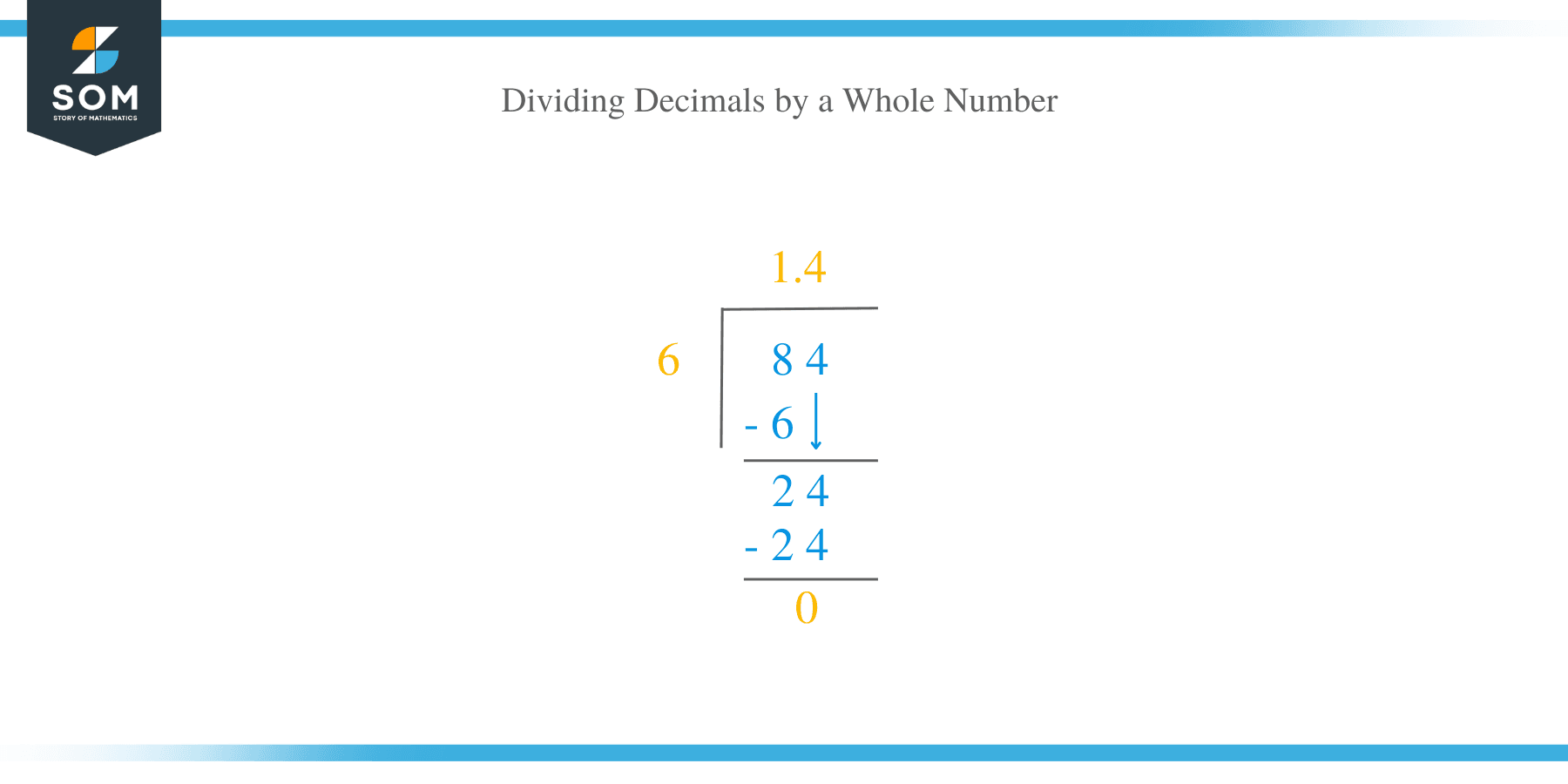
Consider: 8.4 ÷ 6
Suppose we need to find its quotient; the process is carried out as discussed below:
- The first step is to ignore the decimal point in the dividend and rewrite the equation as: 84 ÷ 6
- Carry out the division operation using the regular long division method.
| 14 | |||
| 6 | 84 | ||
| 6 | |||
| 24 -24 = 0 |
In this case, the quotient is 14.
- Therefore, the same number of decimal points are placed in the quotient as they are in the dividend.
- The final answer is 1.4

Example 2
Divide 0.625 by 25.
Solution
- Ignore the decimal point and treat the decimal as whole number: 625 ÷ 25
- Now perform the division operation using the regular long division method.
- 625 ÷ 25 =25
- Since the dividend has 3 decimal places, therefore the quotient will also contain 3 decimal places
- Insert 3 decimal places in the quotient, begin counting from the right going to the left of the quotient.
- The final answer is, 0.025.
How to Divide Decimals by a Decimal Number?
In this case, both the dividend and the divisor are decimal numbers. The division of a decimal number by another decimal number can be performed in the following method:
- The number of decimal places in the divisor is counted.
- The number of decimals in the divisor are inserted in the dividend starting from the decimal point going to the right
- The divisor is then written without a decimal point while the dividend acquires new decimal places.
- Division is carried out as usual using the long division method
- Place the same number of decimal places in the quotient as there are in the new dividend.
Example 3
Divide 8.005 ÷ 0.05
Solution
- The divisor, 0.05 has two decimal places, therefore insert the same number of points in the dividend beginning from the decimal point and going to the right.
- Our new dividend and divisor are now 800.5 and 5 respectively:5 ÷ 5
- Perform the division as usual 5 ÷ 5
- Treat the new dividend as a whole number. 8005 ÷ 5 =1601
- Place the same number of decimal places as they are in the new dividend
- The final answer is, 160.1.