Dividing Complex Numbers – Techniques, Explanation, and Examples

When dividing complex numbers, we make use of our knowledge of conjugates and rationalization of rational expressions. When we find the quotient of two complex numbers, we actually return a fraction that contains these two complex numbers as their numerator and denominator, respectively.

The steps required in dividing complex numbers resemble the process of rationalizing the denominator.

Dividing complex numbers begins by us writing the ratio of the two complex numbers in fraction form.

Most of the techniques needed to divide two complex numbers rely on lessons and skills we’ve learned in the past. Here are some resources you might want to check in case you need a refresher:

• Knowing how to multiply complex numbers is a must if we want to divide complex numbers.
• Understanding how conjugates play an important role in rationalizing denominators and eliminating $i$ from the denominator.

In the next section, you’ll see how complex numbers’ quotient can be manipulated so that the denominator of the quotient contains no complex numbers. We’ll also practice our skills in multiplying complex numbers, so please review your notes.

How to divide complex numbers?

Given two complex numbers, $a + bi$ and $m + ni$, we can express its quotient by dividing $a + bi$ by $m + ni$. Writing it as a ratio, we have $ \dfrac{a + bi}{m + ni}$.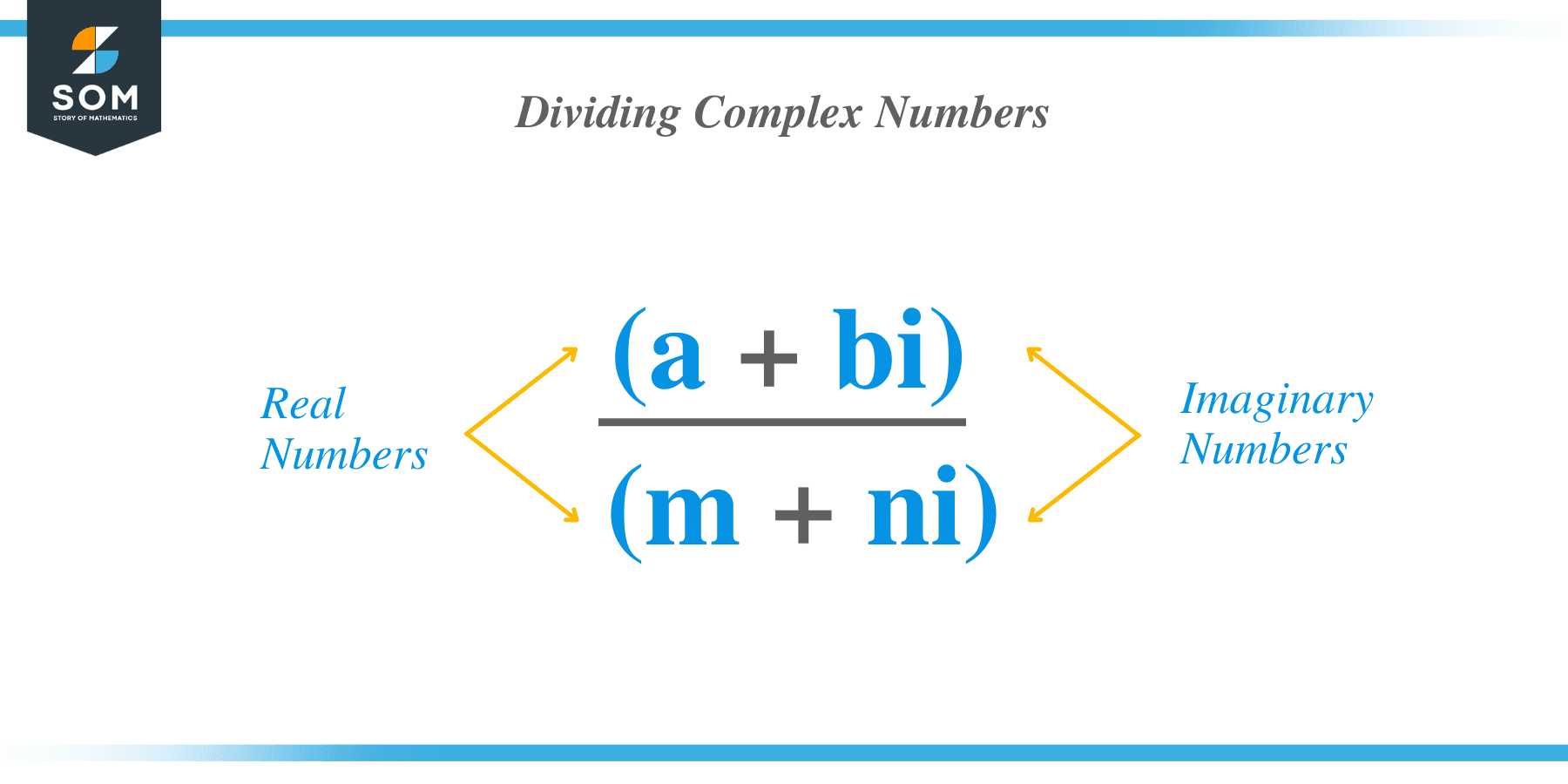

This is the general form of two complex numbers’ quotient. There are three possible forms for the divisor, $m$ and $n$, and the degree of difficulty will depend on which of the values ($m$ and $n$) are present.

Complex number division techniques

Case 1: When $\boldsymbol{n = 0}$

The easiest cases occur when the imaginary number part of the complex number is not present. Given $\dfrac{a+ bi}{m + ni}$, when $n = 0$ , we simply divide $a$ and $bi$ by $n$.

For example, if we want to divide $4 – 12i$ by $4$, we divide each term by $4$ to find their quotient.

$ \begin{aligned} \dfrac{4 – 12i}{4} &= \dfrac{4}{4} – \dfrac{12i}{4}\\&=1 – 4i\end{aligned}$

Case 2: When $\boldsymbol{m = 0}$

Let’s now look when we only have the imaginary part in the denominator (meaning the real number is not present or $m = 0$). We can multiply both numerator and denominator by $i$ and use the fact that $i^2 = -1$.

$ \begin{aligned} \dfrac{a + bi}{ni} &= \dfrac{a + bi}{ni} \cdot \dfrac{i}{i}\\&=\dfrac{i(a + bi)}{i(ni)}\\&= \dfrac{ai + bi^2}{ni^2} \\&= \dfrac{ai + b(-1)}{n(-1)}\\&=\dfrac{ai – b}{-n}\\&= \dfrac{b – ai}{ni}\end{aligned}$

This is the general form of all quotients that belong in this case.

Case 3: When both $\boldsymbol{m}$ and $\boldsymbol{ni}$ are present

When we have a quotient of the form, $\dfrac{a + bi}{m + ni}$, here are steps we’ll keep in mind when simplifying this quotient and rewriting it, so the denominator contains no imaginary part.

1. Multiply both the numerator and denominator of the fraction by the denominator’s conjugate.
2. Expand and simplify the numerator using the FOIL method (or the distributive property when the numerator has one term).
3. Simply the denominator using the property, $(p – qi)(p + qi) = p^2 + q^2$.
4. Express the new form in the lowest terms.

Let’s try to find the quotient of $(3 – 2i)$ and $(5 – i)$ using the four-step guide. We can express their quotient as $\dfrac{3 – 2i}{5 – i}$, so we can multiply both the numerator and denominator by the conjugate of $5 – i$, which is $5 + i$.

$ \begin{aligned} \dfrac{3 – 2i}{5 – i} &= \dfrac{3 – 2i}{5 – i} \cdot \dfrac{\color{blue}5 + i}{\color{blue}5 + i} \\&= \dfrac{(3 -2i)({\color{blue}5 + i})}{(5 – i)({\color{blue}5 + i})}\end{aligned}$

We’ve multiplied both numerator and denominator by $5 + i$, so let’s now apply the FOIL method to multiply the numerator’s complex numbers. Simplify the denominator using the fact that the product of the conjugates is equal to the sum of the squares of their coefficients.

$ \begin{aligned} \dfrac{(3 -2i)(5 + i)}{(5 – i)(5 + i)} &= \dfrac{3(5) + 3(i)+ 5(-2i)+ i(-2i)}{(5 – i)(5 + i)}\\&= \dfrac{15 + 3i – 10i – 2i^2}{(5 – i)(5 + i)}\\&= \dfrac{15 + 3i – 10i + 2}{(5 – i)(5 + i)}\\&= \dfrac{(15 + 2) + (3 – 10)i}{(5 – i)(5 + i)}\\&=\dfrac{17 – 7i}{(5 – i)(5  + i)}\\&= \dfrac{17 – 7i}{5^2 + 1^2}\\&= \dfrac{17 – 7i}{26}\end{aligned}$

Hence, the quotient of $(3 – 2i)$ and $(5 – i)$ is equal to $\dfrac{17 – 7i}{26}$ or $\dfrac{17}{26} – \dfrac{7}{26}i$.

We’ll apply similar steps when finding the quotient and eliminating any imaginary numbers in the denominator of the quotient.

Example 1

Evaluate and simplify the following expressions.

a. $\dfrac{6 – 30i}{2}$
b. $\dfrac{15i + 45}{-3}$
c. $\dfrac{4 – 3i}{\sqrt{2}}$

Solution

Divide each term of the numerator by the denominator since we’re working real number parts only.

For the first expression, we divide $6$ and $30i$ by $2$.

$\begin{aligned} \dfrac{6 – 30i}{2}&= \dfrac{6}{2}- \dfrac{30i}{2}\\&=3 – 15i\end{aligned}$

a. This means that the quotient of $6 – 30i$ and $2$ is $3 – 15i$.

We’ll apply the same process to divide $15i + 45$ by $-3$. Just be careful when working with negative numbers and double-check your work.

$\begin{aligned} \dfrac{15i + 45}{-3}&= \dfrac{15i}{-3}- \dfrac{45}{-3}\\&=-5i – (-15)\\&= -5i + 15\\&= 15 – 5i\end{aligned}$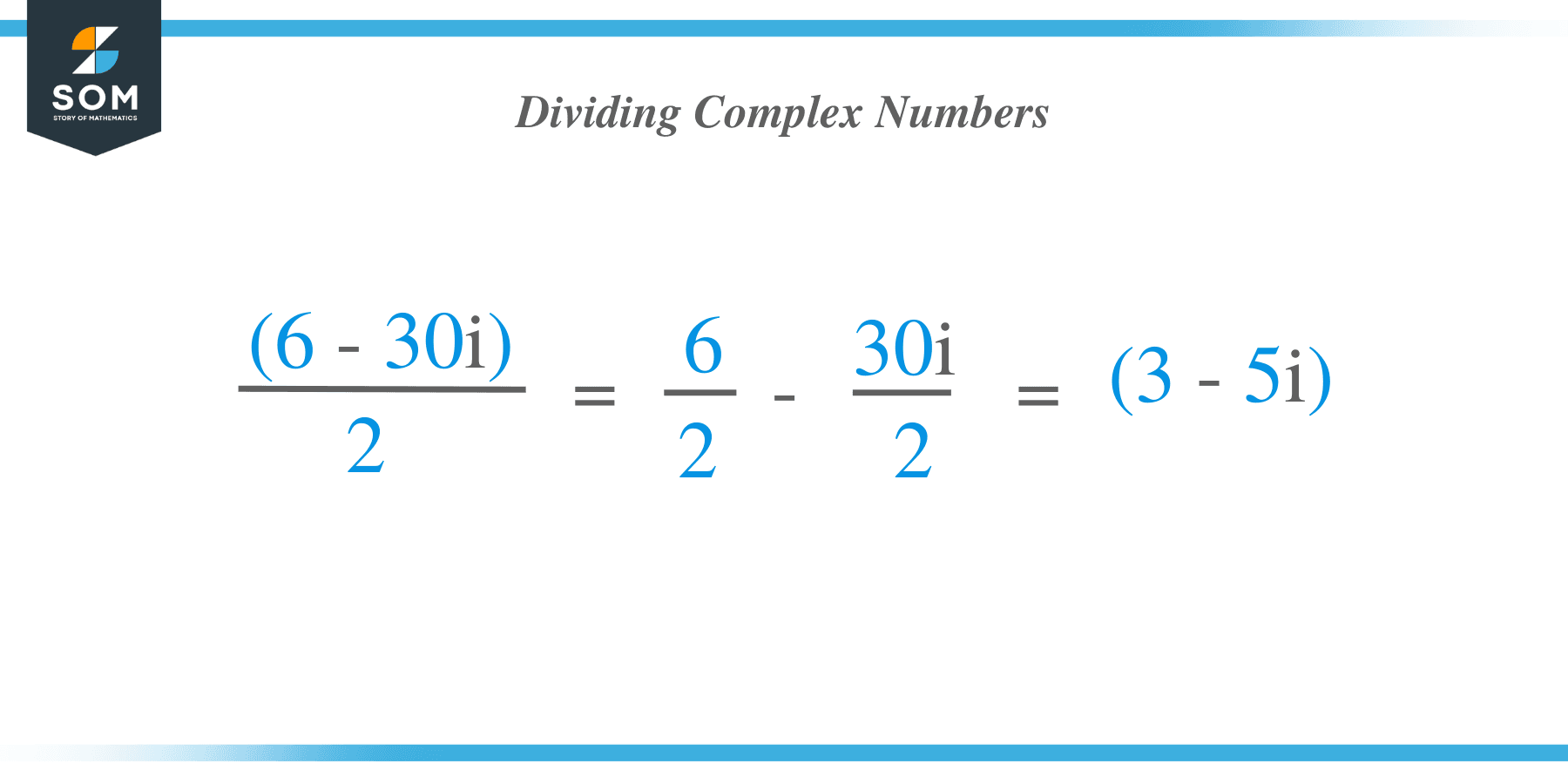

b. Hence, $\dfrac{15i + 45}{-3} = 15 – 5i$.

First, let’s rationalize $\dfrac{4 – 3i}{\sqrt{2}}$ by multiplying both the numerator and the denominator by $\sqrt{2}$.

$\begin{aligned} \dfrac{4 – 3i}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}&= \dfrac{4 \sqrt{2} – 3\sqrt{2}i}{2}\end{aligned}$

We can then divide each term in the numerator by $2$ to express the resulting quotient in the general form of complex numbers.

$\begin{aligned}\dfrac{4 \sqrt{2} – 3\sqrt{2}i}{2}&= \dfrac{4 \sqrt{2}}{2} – \dfrac{3\sqrt{2}i}{2}\\&= 2\sqrt{2} – \dfrac{3\sqrt{2}}{2}i\end{aligned}$

c. This means that $\dfrac{4 – 3i}{\sqrt{2}} = 2\sqrt{2} – \dfrac{3\sqrt{2}}{2}i$.

Example 2

Evaluate and simplify the following expressions.

a. $\dfrac{2 – 5i}{6i}$
b. $\dfrac{12i + 48}{-12i}$
c. $\dfrac{8 – 3i}{\sqrt{3}i}$

Solution

The denominator of each of the quotient only contains an imaginary part, so what we can do is multiply $i$ to each of their numerator and denominator.

Why don’t we start with $\dfrac{2 – 5i}{6i}$? Make sure to also replace $i^2$ with $-1$.

$\begin{aligned}\dfrac{2 – 5i}{6i} \cdot \dfrac{i}{i}&= \dfrac{(2 – 5i)i}{(6i)i}\\&=\dfrac{2i – 5i^2}{6i^2}\\&= \dfrac{2i – 5(-1)}{6(-1)}\\&= \dfrac{2i + 5}{-6}\\&=-\dfrac{5}{6}-\dfrac{2i}{6}\\&= -\dfrac{5}{6} – \dfrac{1}{3}i\end{aligned}$

a. Hence, the quotient of $2 – 5i$ and $6i$ is equal to $-\dfrac{5}{6} – \dfrac{1}{3}i$.

We do the same for b, so multiply both the numerator and denominator of $\dfrac{12i + 48}{-12i}$ by $i$.

$\begin{aligned}\dfrac{12i  +48}{-12i} \cdot \dfrac{i}{i} &= \dfrac{12i^2 + 48i}{-12i^2}\\&=\dfrac{12(-1) + 48i}{-12(-1)}\\&= \dfrac{-12 + 48i}{12}\end{aligned}$

Since all the terms in the numerator and denominator share a common factor of $12$, we can divide all the terms by $12$ to simplify the quotient further.

$\begin{aligned} \dfrac{-12 + 48i}{12} &= \dfrac{-12}{12} + \dfrac{48}{12}i\\&=-1  +4i\end{aligned}$

b. This means that $\dfrac{12i + 48}{-12i}$ is equal to $-1 + 4i$.

The third expression is a bit trickier since the denominator also contains $\sqrt{3}$. Instead of $i$, we multiply both the numerator and denominator by $\sqrt{3} i$ instead.

$\begin{aligned}\dfrac{8 – 3i}{\sqrt{3}i} \cdot \dfrac{\sqrt{3}i}{\sqrt{3}i} &= \dfrac{8\sqrt{3}i – 3\sqrt{3}i^2}{(\sqrt{3} \cdot \sqrt{3})(i \cdot i)}\\&= \dfrac{8\sqrt{3}i – 3\sqrt{3}i^2}{3i^2}\\&= \dfrac{8\sqrt{3}i – 3\sqrt{3} (-1)}{3(-1)}\\&= \dfrac{3\sqrt{3} + 8\sqrt{3}i}{-3}\\&= -\sqrt{3}- \dfrac{8\sqrt{3}}{3}i\end{aligned}$

c. Hence, the simplified form of $\dfrac{8 – 3i}{\sqrt{3}i}$ is $-\sqrt{3}- \dfrac{8\sqrt{3}}{3}i$.

Example 3

What is the result if $4 – 5i$ is divided by $2 – 3i$?

Solution

We can write the quotient in the factored form with the dividend,$4 – 5i$, written on the numerator and the divisor, $2 – 3i$, in the denominator.

Hence, we have $\dfrac{4 – 5i}{2 – 3i}$. Since the denominator is still a complex number, to rewrite this, we can multiply both the numerator and the denominator by the conjugate of $2 – 3i$.

$\begin{aligned}\dfrac{4 – 5i}{2 – 3i} &= \dfrac{4 – 5i}{2 – 3i} \cdot \dfrac{\color{blue} 2 + 3i}{\color{blue} 2 + 3i}\\ &= \dfrac{(4 – 5i)({\color{blue} 2+ 3i})}{(2 – 3i)({\color{blue} 2+ 3i})} \end{aligned}$

Apply the FOIL method to the numerator to simplify the expression.

$\begin{aligned}\dfrac{(4 – 5i)(2 + 3i)}{(2 – 3i)(2 + 3i)} &= \dfrac{4(2) + 4(3i) + 2(-5i) + 3i(-5i)}{(2 – 3i)(2 + 3i)}\\&= \dfrac{8 + 12i – 10i – 15i^2}{(2 – 3i)(2 + 3i)}\\&= \dfrac{8 + 12i – 10i – 15(-1)}{(2-3i)(2 + 3i)}\\&= \dfrac{(8 + 15) +(12 – 10)i}{(2-3i)(2 + 3i)}\\&=\dfrac{23 + 2i}{(2-3i)(2 + 3i)}\end{aligned}$

Simplify the denominator by multiplying the two conjugates.

$\begin{aligned}\dfrac{23 + 2i}{(2-3i)(2 + 3i)} &= \dfrac{23 + 2i}{(2)^2 + (3)^2}\\&=\dfrac{23+ 2i}{4 + 9}\\&= \dfrac{23 + 2i}{13}\\&= \dfrac{23}{13}+ \dfrac{2}{13}i\end{aligned}$

Example 4

Evaluate and simplify $\dfrac{12}{3 – \dfrac{2}{i}}$.

Solution

This expression is a complex fraction that contains an imaginary part in the denominator of $\dfrac{2}{i}$. Let’s focus on eliminating $i$ in the denominator by multiply both the numerator and denominator of $\dfrac{2}{i}$ by $i$.

Use the fact that $i^2$ is equal to $-1$ to simplify the resulting expression further.

$ \begin{aligned}\dfrac{2}{i} \cdot \dfrac{i}{i} &= \dfrac{2i}{i^2}\\&= \dfrac{2i}{-1}\\&= -2i\end{aligned}$

Replace $\dfrac{2}{i}$ with $-2i$, and we’ll end up with another complex number in the denominator.

$\begin{aligned} \dfrac{12}{3 – \dfrac{2}{i}}&= \dfrac{12}{3 – (-2i)}\\&=\dfrac{12}{3 + 2i} \end{aligned}$

Rewrite the quotient by multiplying both its numerator and denominator by the conjugate of $3 + 2i$, which is $3 – 2i$.

$ \begin{aligned} \dfrac{12}{3 + 2i} &= \dfrac{12}{3 + 2i} \cdot \dfrac{\color{blue} 3 – 2i}{\color{blue} 3 – 2i}\\&= \dfrac{12({\color{blue} 3 – 2i})}{(3 + 2i)({\color{blue} 3 – 2i})}\\&= \dfrac{12(3) – 12(2i)}{(3 + 2i)(3 – 2i)}\\&= \dfrac{36 – 24i}{(3 + 2i)(3 – 2i)}\end{aligned}$

Simplify the denominator by finding the product of the two conjugates.

$ \begin{aligned} \dfrac{36 – 24i}{(3 + 2i)(3 – 2i)} &= \dfrac{36 – 24i}{(3)^2 + (2)^2}\\&= \dfrac{36 – 24i}{9 + 4}\\&= \dfrac{36 – 24i}{13}\\&= \dfrac{36}{13}- \dfrac{24}{13}i\end{aligned}$

This means that when simplified, $\dfrac{12}{3 – \dfrac{2}{i}}$ is equivalent to $\dfrac{36}{13}- \dfrac{24}{13}i$.