Difference Quotient – Definition, Formula, & Examples

When you hear of the difference quotient, what are the math concepts that you have in mind? What’s an algebra concept that involves differences and quotients? Well, if you guessed slope, you’re actually close to the definition of the difference quotient.

The difference quotient measures the slope of a secant line passing through the curve of $f(x)$.

There are two important keywords here that we need to understand: slope and secant line.

A linear function’s slope represents the measure of its “rise over run”. What does this mean mathematically?

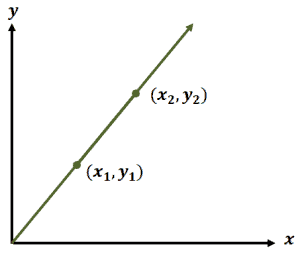
Slopes (normally represented as $m$) are calculated by finding the difference between two given points’ $y$-coordinates and $x$-coordinates then taking the quotient of the two.

$m=\dfrac{y_2 – y_1}{x_2 – x_ 1}$

Now, what are secant lines? They are the lines that pass through a figure or a graph at exactly two points.

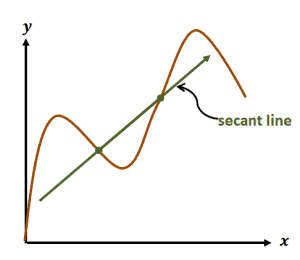
The graph shown above is an example of a secant line passing through a curve. As you can see, the secant line passes through two points along the curve.

Now that we’ve reviewed these important concepts, it’s that we learn more about difference quotients.

What is the difference quotient?

The difference quotient of a function measures the average rate of change of $f(x)$ with respect to x given an interval, $[a, a + h]$.

Given a function, $f(x)$, its difference quotient tells us the slope of the line that passes through two points of the curve: $(a, f(a))$ and $((a+h), f(a+h))$. Let’s visualize this to better understand the concept of the difference quotient.

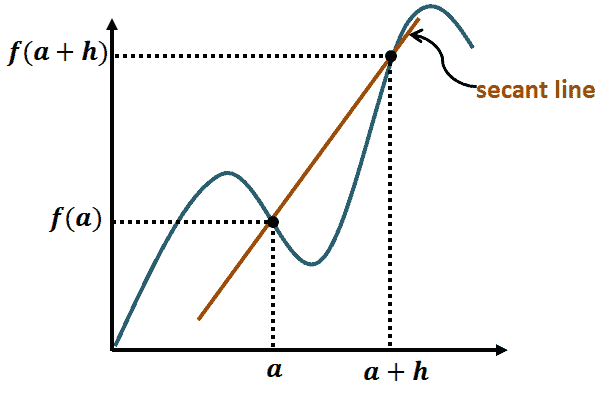
As can be seen from the graph shown, the difference quotient measures the slope of the line passing through $a$ and $a + h$.

Understanding the difference quotient formula

So, how do we apply this definition and calculate for the difference quotient of a function given a secant line? We use our knowledge of slope to establish the formula for the difference quotient.

Let’s determine the function’s value at $a + h$ and $a$. Once we have the values, we find the difference between the two to find the “rise” of the function or $\Delta y$ at those two points.

$\Delta y = f(a+h) – f(a)$

The difference between the two intervals represents the slope’s run or $\Delta x$. Hence, we have

$\Delta x = (a+h) – a = h$

With these two, we can now write the formula for the difference quotient as

$\dfrac{\Delta y}{\Delta x} = \dfrac{f(a+h) – f(a)}{h}$

How to evaluate difference quotient?

$\dfrac{\Delta y}{\Delta x} = \dfrac{f(a+h) – f(a)}{h}$

Now that we know the difference quotient’s definition and formula, it’s time that we learn how to actually apply them. Here are four steps to remember when evaluating difference quotients:

1. Find the expression of $f(a+h)$ by substituting $x$ in $f(x)$ with $a + h$.
2. Find the expression of $f(a)$ by substituting $x$ in $f(x)$ with $a$.
3. Find the difference between the two.
4. Divide the expression by $h$.

Let’s try to evaluate $f(x) = \Delta x$. Start by finding $f(a + h)$:

$ \begin{aligned}f(a) &= 4a \\ f(a + h) &= 4(a + h)\\ &= 4(a) + 4(h)\\ &= 4a + 4h\end{aligned}$

Subtract $f(a + h)$ and $f(a)$ then divide the result by $h$:

$\begin{aligned}\dfrac{f(a+h) – f(a)}{h} &=  \dfrac{4a + 4h – 4a}{h}\\ &= \dfrac{4h}{h} \\&=4\end{aligned}$

This means that the difference quotient of $f(x) = 4x$ is $4$.

How to simplify difference quotient?

We’ve worked out the difference quotient of $f(x) = 4x$. Now, what if we’re working on more complicated functions?

The same process will be applied, but it’s important for us to remember the tricks and techniques in simplifying algebraic expressions.

• When simplifying the numerator, $f(a+h) – f(a)$, make sure to distribute the negative signs correctly.
• Factor out $h$ from the numerator whenever possible.
• When working with quadratic expressions, remember the algebraic property, $(m \pm n)^2 = m^2 \pm 2mn + n^2$.
• Apply the FOIL method whenever possible too.
• When adding two rational expressions, rewrite the functions so that they share a common denominator.
• Do your best to simplify the numerator first. Remember, $\dfrac{f(a+h) – f(a)}{h} = \dfrac{1}{h} \cdot [f(a+h) – f(a)]$, so you can focus on the denominator later.

Now that we have these helpful tips, let’s try to simplify the difference quotient of the function shown below.

$f(x) = \dfrac{1}{x^2}$

We begin by finding the expression for $f(a+h)$. Substitute $a+h$  into the expression for x and apply the algebraic property, $(m \pm n)^2 = m^2 \pm 2mn + n^2$.

$f(a + h) = \dfrac{1}{ (a + h)^2}$

Find the difference between $f(a + h)$ from the expression of $f(a)$. Rewrite the two fractions so that they share a common denominator.

$f(a + h) – f(a) = \dfrac{1}{ (a + h)^2} – \dfrac{1}{ a^2}$

Rewrite the two fractions so that they share a common denominator.

$=  \dfrac{a^2}{a^2(a + h )^2}– \dfrac{(a + h )^2}{a^2 (a + h)^2}$

Combine the numerators and expand the factored expressions using $(m \pm n)^2 = m^2 \pm 2mn + n^2$. Don’t forget to distribute the negative signs!

$   \begin{aligned} =  \dfrac{a^2 – (a + h )^2}{a^2 (a + h )^2} &=  \dfrac{a^2 – (a^2 + 2ah + h^2)}{a^2 (a + h )^2}\\&=  \dfrac{a^2 – a^2 – 2ah – h^2}{a^2 (a + h )^2}\\ &=  \dfrac{– 2ah – h^2}{a^2 (a + h )^2}\\ &= \dfrac{-h(2a + h)}{a^2 (a + h )^2}\end{aligned}$

To find the difference quotient, let’s divide the resulting expression by $h$.

$\begin{aligned}\dfrac{f(a+h) – f(a)}{h } &=  \dfrac{\dfrac{1}{(a + h )^2}  – \dfrac{1}{a^2}}{ h}\\ &= \dfrac{– h(2a + h)}{a^2 (a + h )^2}{h}\\ &= \dfrac{1}{h} \cdot  \dfrac{– h(2a + h)}{a^2 (a + h )^2}\end{aligned}$

Cancel out common factors to further simplify the difference quotient.

$  \dfrac{f(a+h) – f(a)}{h} =  -\dfrac{ (2a + h)}{a^2 (a + h )^2}$

This means that the difference quotient of $f(x) = \dfrac{1}{x^2}$ is$-\dfrac{2a + h}{a^2 (a + h )^2}$.

Don’t worry, the last example will also be easy once we practice more problems involving difference quotients.

The next few examples will also help you strengthen your algebraic skills and also, help you master the steps in finding the difference quotients of various functions.

Example 1

If $f (a + h) = 4a + 4h + 3$ and $f(a) = 4a + 3$, which of the following statements is not true?

1. The function, $f(x)$, is equal to $4x + 3$.
2. The difference between $f (a)$ and $f (a + h)$ is $4h$.
3. The difference quotient of $f(x)$ is $4$.
4. The difference quotient of $f(x)$ is $4h$.

Solution

To confirm whether $f(x)$ is actually equal to $4x + 3$, let’s compare $f(a)$ and the factored form of $f(a + h)$:

$\begin{aligned} f (a) &= 4a + 3 \\f (a + h) &= 4(a + h) + 3\end{aligned}$

From this, we can see that $f(x)$ is equal to $4x + 3$. This confirms that (a) is a true statement.

Let’s go ahead and subtract the two given expressions.

$ \begin{aligned}f (a + h) – f(a)  &= 4a + 4h + 3 – (4a + 3)\\ &= 4a + 4h + 3 – 4a – 3\\ &= 4h\end{aligned}$

This means that (b) is correct.

Find the difference quotient by dividing the $f (a + h) – f(a)$  by $h$.

$ \begin{aligned}\dfrac{f (a + h) – f(a)}{h}  &= \dfrac{4h}{h}\\ &=4\end{aligned}$

This means that the correct statement between (c) and (d) is (c), so the statement that is not correct is (d).

 Example 2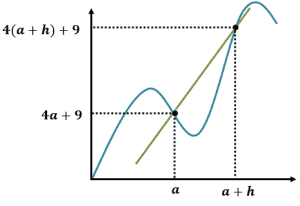

What is the difference quotient of the function represented by the graph shown?

Solution

When working with problems that involve the difference quotient, let’s also go back to its definition:

Difference Quotient $=\dfrac{f (a + h) – f(a)}{h}$

Since both $f(a) $ and $f(a + h)$ are already given, let’s go ahead and subtract the two expressions. Note: it’s important to double-check when distributing the negative sign.

$ \begin{aligned}f(a+h) – f(a) &= 4(a + h) + 9 – (4a + 9) \\ &= 4a + 4h + 9 – 4a – 9\\ &= 4h \end{aligned}$

Divide the resulting difference by $h$ to find the difference quotient.

Difference Quotient $= \dfrac{4h}{h} = 4$

This means that the function shown has a difference quotient of $4$.

Example 3

What is the difference quotient of the function represented by the graph shown below?

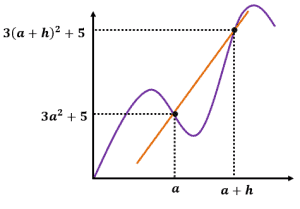
Solution

This is a similar problem, but this time, we’re working with a more complex expression. Let’s go ahead and write the difference quotient formula:

Difference Quotient $=\dfrac{f (a + h) – f(a)}{h}$

Since both $f(a)$ and $f(a + h)$ are also given, let’s go ahead and subtract the two expressions. Since the first term is a squared binomial, we can expand it using the algebraic property, $(m \pm n)^2 = m^2 \pm 2mn + n^2$.

$\begin{aligned} f(a+h) – f(a) &= 3(a + h)^2 + 5 – (3a^2 + 5)\\ &= 3(a^2 + 2ah + h^2) + 5 – 3a^2 – 5\end{aligned}$

Distribute $3$ into the parenthesis and combine like terms.

$\begin{aligned}&= 3a^2 + 6ah + 3h^2 + 5 –3a^2 – 5\\ &= 6ah + 3h^2\end{aligned}$

Once we have the simplified difference, let’s divide the expression by $h$.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{f(a+h) – f(a)}{h}\\ &= \dfrac{6ah + 3h^2}{h }\\&= 6a + 3h \end{aligned}$

This means that $3x^2 + 5$ has a difference quotient of $6a + 3h$.

Example 4

What is the difference quotient of the function $f(x) = 3(x + 1) – 5$?

Solution

When finding the difference quotient of a function, let’s begin by finding $f(a)$ and $f(a + h)$.

$\begin{aligned} f(a) &= 3(a + 1) – 5\\ &= 3a + 3 – 5\\ &= 3a – 2\\\\f(a + h)  &= 3(a + h + 1) – 5\\ &= 3a + 3h + 3 – 5\\ &= 3a + 3h – 2\end{aligned}$

Find the difference between the two expressions.

$\begin{aligned} f(a+h) – f(a) &= 3a + 3h – 2  – (3a – 2)\\ &= 3a + 3h – 2  – 3a + 2\\ &= 3h\end{aligned}$

 Now that we have the difference, let’s divide the expression by $h$ to find the difference quotient of $f(x)$.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{f(a+h) – f(a)}{h}\\ &= \dfrac{3h}{h} \\&= 3\end{aligned}$

This means that $f(x) = 3(x + 1) – 5$ has a difference quotient of $3$.

Example 5

What is the difference quotient of the function $f(x) = x^2 – 4x + 3$?

Solution

When finding the difference quotient of a function, let’s begin by finding $f(a)$ and $f(a + h)$.

$ \begin{aligned}f(a) &= a^2 – 4a + 3\\f(a + h)  &= (a + h)2 – 4(a + h) + 3 \end{aligned}$

Expand $f(a + h)$ using the algebraic property, $(m ± n)^2 = m^2 \pm  2mn + n^2$. Distribute $4$ in the second group then combine like terms.

$ \begin{aligned}f(a + h)  &= (a^2 + 2ah + h^2) – 4(a + h) + 3\\ &= a^2 + 2ah + h^2 – 4a – 4h + 3\\ &= a^2 + 2ah + h^2 – 4a – 4h + 3\end{aligned}$

Find the difference between the two expressions.

$\begin{aligned} f(a+h) – f(a) &= a^2 + 2ah + h^2 – 4a – 4h + 3 – (a^2 – 4a + 3)\\ &= a^2 + 2ah + h^2 – 4a – 4h + 3 – a^2 + 4a – 3\\ &= h^2+ 2ah – 4h\end{aligned}$

Now that we have the difference, let’s divide the expression by $h$ to find the difference quotient of $f(x)$.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{h^2+ 2ah – 4h}{h}\\ &= h + 2a – 4\end{aligned}$

This means that $f(x) = x^2 – 4x + 3$ has a difference quotient of $h + 2a – 4$.

Break time! How are you doing so far? Don’t forget to double-check your calculations (especially for tricky numerators). Make use of properties as much as you can and if you think you need some refresher, take your old resources out (our site has a lot or resources too!) and review some techniques that may help.

Let’s continue and work with more complicated expressions and answer some word problems as well.

Example 6

What is the difference quotient of the function $f(x) = \dfrac{1}{4x}$?

Solution

Working with rational expressions may appear intimidating at first when finding the difference quotient of a function. This example will show how, with the right technique, we can actually manipulate the expressions faster. What are we waiting for? Let’s begin!

Find the expressions of $f(a)$ and $f(a + h)$.

$ \begin{aligned}f(a) &= \dfrac{1}{4a}\\ f(a + h)  &= \dfrac{1}{4(a + h)}\end{aligned}$

No need to expand $f(a + h)$ first and let’s proceed to finding the difference of $f(a)$ and $f(a + h)$. Rewrite each expression so that they share a common denominator, $4a(a + h)$, then combine the terms in the numerator.

$\begin{aligned} f(a+h) – f(a) &= \dfrac{1}{4(a + h)}  –  \dfrac{1}{4a}\\ &= \dfrac{a}{4a(a + h)} – \dfrac{a + h}{4a(a + h)}\\ &=\dfrac{a – (a + h)}{4a(a + h)}\\ &= \dfrac{a – a – h}{4a (a + h)}\\&= -\dfrac{h}{4a (a + h)}\end{aligned}$

Now that we have the difference, let’s divide the expression by $h$ to find the difference quotient of $f(x)$. Remember that we can instead multiply the difference by $\dfrac{1}{h}$ to find the quotient.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{h^2+ 2ah – 4h}{h}\\  = \dfrac{1}{h} \cdot -\dfrac{h}{4a (a + h)}\end{aligned}$

We can then cancel out $h$ to simplify the quotient.

$=-\dfrac{1}{4a(a + h)}$

This means that $f(x) = \dfrac{1}{4x}$ has a difference quotient of $-\dfrac{1}{4a(a + h)}$ or $-\dfrac{1}{4a^2 + 4ah}$.

Example 7

What is the difference quotient of the function $f(x) = \dfrac{2x}{3-x}$?

Solution

Here’s another rational expression for us to work on. Let’s go ahead and find the expressions of $f(a)$ and  $f(a + h)$.

$\begin{aligned} f(a) &= \dfrac{2a}{3 – a}\\ f(a + h)  &= \dfrac{2(a + h)}{3- (a+h)} \\ &= \dfrac{(2a + 2h)}{3 – a -h}\end{aligned}$

Now, let’s subtract the $f(a)$ and $f(a + h)$. We can do this by first rewriting each fraction so that they share their common denominator, $(3 – a – h)(3 – a)$.

$\begin{aligned} f(a+h) – f(a) &= \dfrac{2a + 2h}{3 –  a – h} – \dfrac{2a}{3 –  a} \\&= \dfrac{(2a + 2h)(3 – a )}{(3 – a – h)(3 – a)} – \dfrac{\dfrac{2a}{3 – a – h}}{\dfrac{3 – a – h}{(3 – a}}\\&= \dfrac{6a – 2a^2 + 6h – 2ha – (6a – 2a^2 – 2ah)}{(3 – a – h)(3 – a)}\\ &= \dfrac{6h}{(3 – a – h)(3 – a)}\end{aligned}$

We can stop simplifying the difference here and proceed to finding the difference quotient of $f(x)$. Remember that we can instead multiply the difference by $\dfrac{1}{h}$ to find the quotient.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{h^2+ 2ah – 4h}{h}\\  &= \dfrac{1}{h} \cdot \dfrac{6h}{(3- a -h)(3 – a)}\end{aligned}$

We can then cancel out $h$ to simplify the quotient.

$= \dfrac{6}{(3 – a – h)(3 – a)}$

This means that $f(x) = \dfrac{2x}{3 – x}$ has a difference quotient of $\dfrac{6}{ (3 – a – h)(3 – a)}$.

Time for a cool down. Now that we’ve worked our mind muscles in working on these problems, let’s go ahead and slow down by answering the conceptual problems.

Example 7

What is the difference quotient of $f(x) = 8$? How about $g(x) = \pi$? What’s the reason behind their difference quotients?

Solution

Let’s quickly find each of the important components in finding their respective difference quotients.

$f(a) = 8$,               $g(a) = \pi$

$ f(a + h)  = 8$,        $g(a + h)  = \pi$

This means that the difference for each is $0$ and consequently, each of their difference quotients are equal to zero.

The constant functions $f(x)$ and $g(x)$ will always remain constant throughout any given interval. This means that the rate of change in any point of their curves will be zero.

Example 8

The general form of linear functions can be expressed as $f(x) = px + q$, where $p$ and $q$ are nonzero coefficients. Show that the difference quotient of any linear function is equal to the coefficient before $x$.

Solution

Let’s go ahead and express $f(a)$ and $f(a + h)$ in terms of $p$ and $q$.        

$\begin{aligned} f(a) &= pa + q\\ f(a + h)  &= p(a + h) + q\\ &= pa + ph + q\end{aligned}$

Subtract the two expressions and divide the result by $h$.

$\begin{aligned} \text{Difference Quotient} &= \dfrac{h^2+ 2ah – 4h}{h}\\  &= \dfrac{pa + ph + q – (pa + q)}{h}\\ &= \dfrac{ph}{h}\\ &= p\end{aligned}$

We’ve just shown that the difference quotient of $f(x) = px + q$ is $p$ or the coefficient before $x$.