-(a) \[ \alpha = 0.0089 \]
-(b) \[ \alpha = 0.09 \]
-(c) \[ \alpha = 0.707 \]
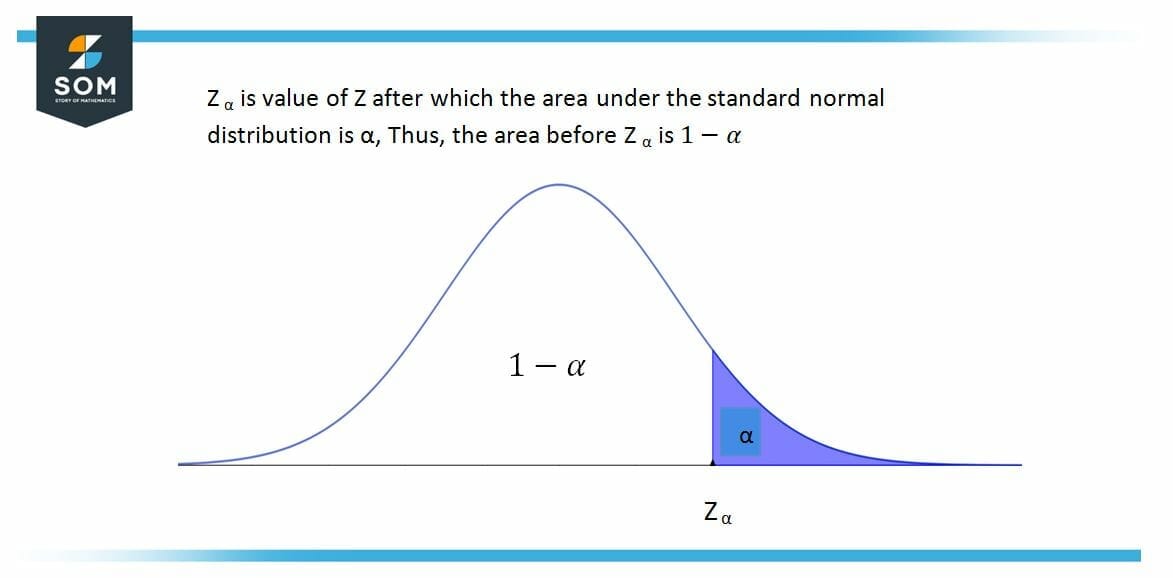In this question, we have to find the value of $ Z_{ \alpha }$ for all the three parts where the value of $ \alpha $ is given already.
The basic concept behind this question is the knowledge of Confidence Level, standard normal probability table, and $Z_{\dfrac{\alpha}{2}}$.
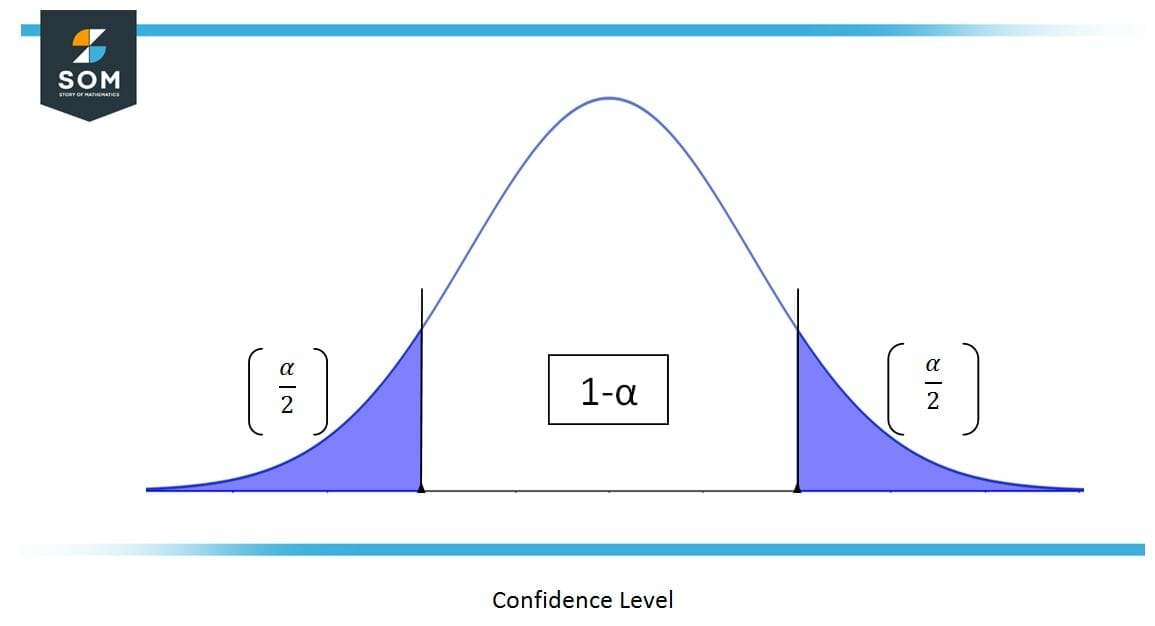In mathematics Confidence Level $ CL $ is expressed as:
\[ c = 1 – \alpha \]
where:
$ c = Confidence\ Level $
$ \alpha $ = no unknown population parameter
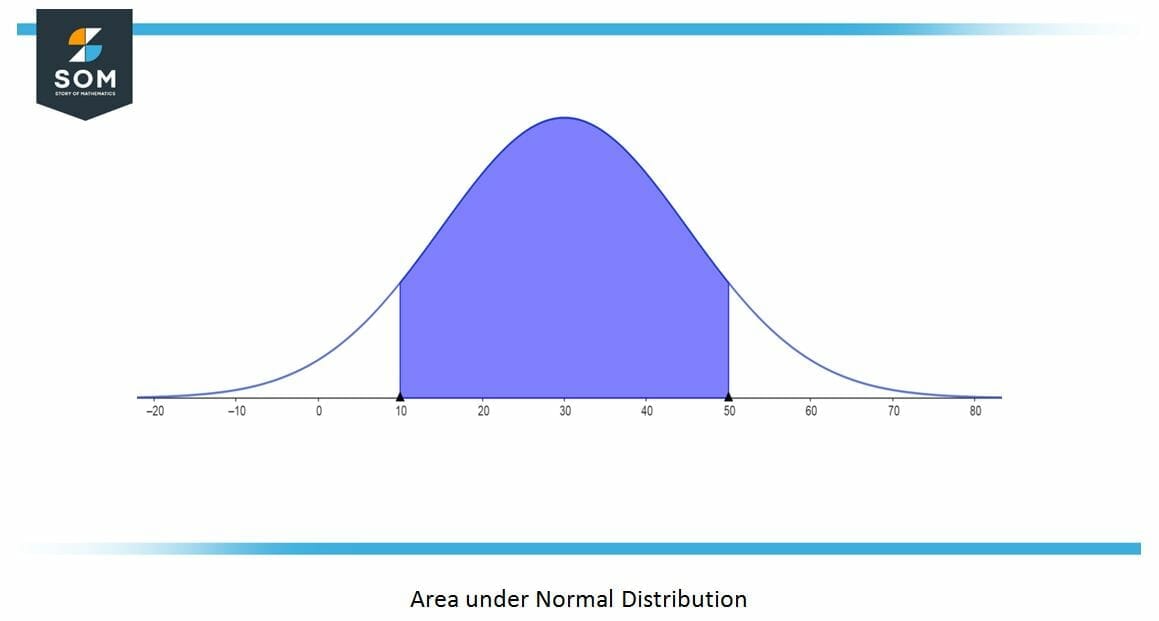$ \alpha$ is the area of the normal distribution curve which is $\frac{\alpha }{ 2 } $ for each side and can be expressed mathematically as:
\[ \alpha = 1- CL \]
Expert Answer
(a) Given the value of $ \alpha$, we have:
\[\alpha\ =\ 0.0089\]
Now putting the value of given $\alpha $ in the central limit formula:
\[ c = 1 -\ \alpha \]
\[ c = 1 -\ 0.0089 \]
\[ c =\ 0.9911 \]
In terms of percentage, we have the Confidence Level:
\[ Confidence\ \space Level = 99.5 \% \]
Now to find the value of $ Z_{ \alpha }$ we will use the help of an excel sheet and put excel function $normsinv(c)$ to get the value of corresponding $ Z- value $
\[ Z_{ \alpha }= normsinv(c) \]
\[ Z_{ \alpha }= normsinv(0.9911) \]
\[ Z_{ \alpha }= 2.37 \]
(b) Given the value of $ \alpha$ we have:
\[\alpha\ =\ 0.09\]
Now putting the value of given $\alpha $ in the central limit formula:
\[ c = 1 -\ \alpha \]
\[ c = 1 -\ 0.09 \]
\[ c =\ 0.91 \]
In terms of percentage, we have the Confidence Level:
\[ Confidence\ \space Level = 91 \% \]
Now to find the value of $ Z_{ \alpha }$ we will use the help of an excel sheet and put excel function $normsinv(c)$ to get the value of corresponding $ Z- value $:
\[ Z_{ \alpha }= normsinv(c) \]
\[ Z_{ \alpha }= normsinv(0.91) \]
\[ Z_{ \alpha }= 1.34 \]
(c) Given the value of $ \alpha$ we have:
\[\alpha\ =\ 0.707\]
Now putting the value of given $\alpha $ in the central limit formula:
\[ c = 1 -\ \alpha \]
\[ c = 1 -\ 0.707 \]
\[ c =\ 0.293 \]
In terms of percentage, we have the Confidence Level:
\[ Confidence\ \space Level = 29.3 \% \]
Now to find the value of $ Z_{ \alpha }$ we will use the help of an excel sheet and put excel function $normsinv(c)$ to get the value of corresponding $ Z- value $:
\[ Z_{ \alpha }= normsinv(c) \]
\[ Z_{ \alpha }= normsinv(0.293) \]
\[ Z_{ \alpha }= -0.545 \]
Numerical Results
\[Z_{\alpha}= 2.37\]
\[Z_{\alpha}= 1.34\]
\[Z_{\alpha}= -0.545\]
Example
Find the confidence level when:
\[\frac{\alpha}{2}=0.0749\]
Solution
\[\alpha=0.0749 \times 2\]
\[\alpha=0.1498\]
\[c=1- \alpha\]
\[c=0.8502\]
\[ Confidence\ \space Level = 85.02 \% \]