
\[\lim_{n\to\infty}\sum_{i=1}^{n}\frac{\pi}{4n}{tan\left(\frac{i\pi}{4n}\right)} \]
The purpose of this article is to find the region having an area under the curve that is represented by a given limit.
The basic concept behind this guide is the use of the Limit Function to determine an area of the region. The area of a region that covered the space above the $x-axis$ and the below the curve of given function $f$ integrable on $a$ to $b$ is calculated by integrating the curve function over a limit interval. The function is expressed as follows:
\[\int_{a}^{b}{f(x)dx} \]
The area of the region enclosed by $x-axis$ and curve function $f$ is expressed in limit form as follows:
\[\int_{a}^{b}{f(x)dx}=\lim_{n\to\infty}\sum_{i=1}^{n}f{(x_i)}∆x \]
Where:
\[x_i=a+i ∆x \]
So:
\[\int_{a}^{b}{f(x)\ dx}\ =\lim_{n\to\infty}\sum_{i=1}^{n} f(a+i∆x) ∆x \]
Here:
\[∆x = \frac{b-a}{n} \]
Expert Answer
Given Function is:
\[\int_{a}^{b}{\ f(x)\ \ dx}\ =\ \lim_{n\to\infty} \sum_{i\ =\ 1}^{n}{\ \frac{\pi}{4n}}{\ tan\ \left(\frac{i\pi}{4n}\right)} \]
We know that the standard form for an area of the region:
\[\int_{a}^{b}{f(x)\ dx}\ =\lim_{n\to\infty}\sum_{i=1}^{n} f(a+i∆x) ∆x \]
Comparing the given function with the standard function, we find the value of each component as follows:
\[a\ +\ i\ ∆x = \frac{i\pi}{4n} \]
Hence:
\[a\ =\ 0 \]
\[∆x = \frac{\pi}{4n} \]
As we know:
\[∆x = \frac{b-a}{n}=\frac{\pi}{4n} \]
\[\frac{b-0}{n}\ =\ \frac{\pi}{4n} \]
\[b\ =\ \frac{\pi}{4} \]
Let’s consider:
\[f(x)\ =\ tan\ (x) \]
So:
\[\lim_{n\to\infty}\sum_{i=1}^{n}\frac{\pi}{4n}{tan\left(\frac{i\pi}{4n}\right)}\ =\ \int_{a}^{b}{\ f(x)\ dx} \]
Substituting the values on the left-hand side of the above expression:
\[\lim_{n\to\infty}\sum_{i=1}^{n}\frac{\pi}{4n}{tan\left(\frac{i\pi}{4n}\right)}\ =\ \int_{0}^{\frac{\pi}{4}}{\ tan\ (x)\ dx\ =\ 0.346} \]
The equation for the curve is:
\[f(x)\ =\ tan\ (x) \]
The interval for $x-axis$ is:
\[x\ \in\ \left[0,\ \frac{\pi}{4}\right] \]
It is represented by the following graph:
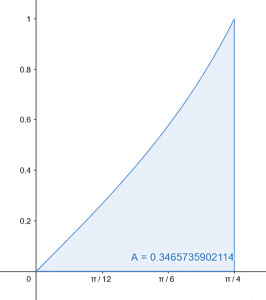
Figure 1
Numerical Result
The region, having an area defined by the given limit, is equal to the region below the following curve function and above $x-axis$ for the given interval, as follows:
\[f(x)\ =\ tan(x),\ \ x\ \in\ \left[0,\ \frac{\pi}{4}\right] \]

Figure 1
Example
Find an expression for the region having an area equal to the following limit:
\[\lim_{n\to\infty}\ \sum_{i\ =\ 1}^{n}{\ \frac{2}{n}}\ {\left(5\ +\ \frac{2i}{n}\right)} \]
Solution
Given Function is:
\[\int_{a}^{b}{\ f(x)\ dx}\ =\ \lim_{n\to\infty}\ \sum_{i\ =\ 1}^{n}{\ \frac{2}{n}}{\ \left(5\ +\ \frac{2i}{n}\right)} \]
We know that the standard form for an area of the region:
\[\int_{a}^{b}{f(x)\ dx}\ =\lim_{n\to\infty}\sum_{i=1}^{n} f(a+i∆x) ∆x \]
Comparing the given function with the standard function, we find the value of each component as follows:
\[a\ +\ i∆x = 5 + i \frac{2}{n} \]
Hence:
\[a\ =\ 5 \]
\[∆x =\frac{2}{n} \]
As we know:
\[∆x = \frac{b-a}{n} \]
\[\frac{b-5}{n}\ =\ \frac{2}{n} \]
\[b\ =\ 7 \]
Let’s consider:
\[f(x)\ =\ 5\ +\ x \]
So:
\[ \lim_{n\to\infty}\ \sum_{i\ =\ 1}^{n}{\ \frac{2}{n}}\ {\left(5\ +\ \frac{2i}{n}\right)}\ =\ \int_{a}^{b}{\ f(x)\ dx} \]
Substituting the values on the left-hand side of the above expression:
\[ \lim_{n\to\infty}\ \sum_{i\ =\ 1}^{n}{\ \frac{2}{n}}\ {\left(5\ +\ \frac{2i}{n}\right)}\ =\ \int_{5}^{7}{\ (5\ +\ x)\ dx} \]
The equation for the curve is:
\[ f(x)\ =\ 5\ +\ x \]
The interval for $x-axis$ is:
\[ x\ \in\ \left[5,\ 7\right] \]
Image/Mathematical drawings are created in Geogebra
