Derivatives of Vectors – Definition, Properties, and Examples

The derivatives of vectors highlight the fact that we can also calculate the rate of change that occurs in vector-valued functions. You’ll see how similar the concepts of derivatives in curve spaces and derivatives in planes are. By mastering this topic, a wide array of mathematical concepts will open for you to learn later as well!

The derivatives of vectors and vector functions are dependent on the derivatives of vector functions’ components. We can also formally define the derivative of vector-valued functions using our formal definition of derivatives from real-valued functions.

In this article, we’ll cover the fundamental definition of derivatives. We’ll also understand the different derivative rules that we can use to differentiate complex products between scalar and vector functions. By the end of the discussion, you’ll be able to work on more complex problems involving derivatives of vector functions.

For now, let’s dive right into the fundamental definition of vectors!

What Are Derivatives of Vectors?      

The derivative of vectors or vector-valued functions can be defined similarly to the way we define the derivative of real-valued functions. Let’s say we have the vector-values function, $\textbf{r}(t)$, we can define its derivative by the expression shown below.

\begin{aligned}\dfrac{d\textbf{r}}{dt} &= \textbf{r}\prime(t)\\&= \lim_{h \rightarrow 0} \dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}\end{aligned}

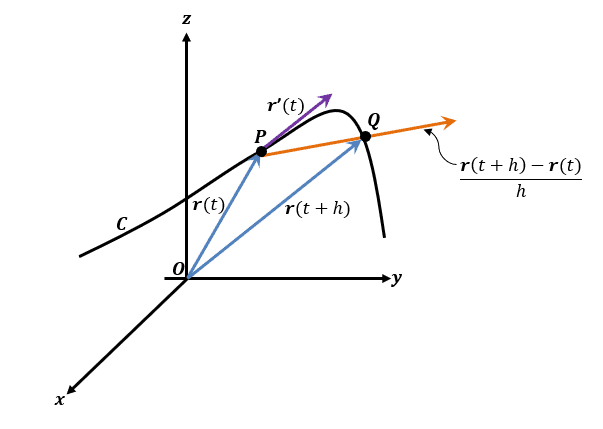
The graph above helps us understand how we can establish the definition of the derivatives for vectors or vector-valued functions. Let’s say we have $P$ and $Q$  are contained within the position vectors, $\textbf{r}(t)$ and $\textbf{r}(t + h)$. This means that we can express $\overrightarrow{PQ}$ as $\textbf{r}(t + h) – \textbf{r}(t)$ and this vector represents the secant vector of the curve.

When $h > 0$, we can see that the $\dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}$ is a scalar multiple of the secant vector. As $h \rightarrow$, we can see the vector lies closer to the tangent vector. This is why we call $\textbf{r}\prime(t)$ as the tangent vector.

\begin{aligned}\textbf{r}(t) &= \left<x(t), y(t), z(t)\right>\\\textbf{r}\prime(t) &= \lim_{h \rightarrow 0} \dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}\\&= \lim_{h \rightarrow 0} \left<\dfrac{x(t + h) – x(t)}{h},\dfrac{y(t + h) – y(t)}{h}, \dfrac{z(t + h) – z(t)}{h}\right>\\&= \left<x\prime(t), y\prime(t), z\prime(t)\right>\end{aligned}

Hence, we can simplify the method of calculating the derivative of the vector function by simply differentiating the components of the vector function.

Here are some other terms that you might encounter when dealing with the derivatives of vectors:

• The tangent line to the curve, $C$, that passes through the point, $P$, can be defined by the tangent vector, $\textbf{r}\prime(t)$.
• We can calculate the unit tangent vector by dividing the derivative of $\textbf{r}\prime(t)$ by the absolute value of $|\textbf{r}\prime(t)$.

\begin{aligned}\textbf{T}(t) &= \dfrac{\textbf{r}\prime(t)}{|\textbf{r}\prime(t)|}\end{aligned}

Now that we know the formal and practical definition of vector derivatives, let’s break down the process of calculating the derivatives of different vector-valued functions!

How To Find Derivatives of Vectors?

Calculate the derivative of a vector-valued function by taking the derivative of the components of the vector functions.

• Differentiate each of the components of the vector function.
• Apply the derivative rules we’ve learned in the past to simplify the derivative of the components.
• Write down the derivative of vector functions by writing down the derivative of the components in form of $\textbf{r}\prime(t) = \left<x\prime(t), y\prime(t), z\prime(t)\right>$ or $\textbf{r}\prime(t) = x\prime(t)\textbf{i} + y\prime(t)\textbf{j} + z\prime(t)\textbf{k}$.

Let us write down the common differentiation formulas for vector-valued functions. These are simply the counterparts for the derivative rules we’ve learned when working on real-valued functions.

From the derivative rules listed on the table, we can see that we have extended the product rule to account for the following conditions:

• Differentiating the product of real-valued and vector-valued functions
• Finding the derivative of the dot product between two vector-valued functions
• Differentiating the cross-product between two vector functions

These differentiation formulas can be proven with derivative properties, but we’ll leave these proofs in the sample problems for you to work on!

For now, let us show you a quick example of differentiating a vector function by finding the derivative of $\textbf{r}(t) = (3t – 4)\textbf{i} + (6t^2 + 4t -1)\textbf{j} + (e^t \sin t) \textbf{k}$.

\begin{aligned}x(t) &= 3t – 4\\ y(t) &= 6t^2 + 4t – 1\\ z(t)&= e^t \sin t\end{aligned}

Differentiate each of the components first by applying the fundamental derivative rules.

Now, use these components to write the derivative of $\textbf{r}\prime(t)$.

\begin{aligned}\textbf{r}\prime(t) &= x\prime(t)\textbf{i} + y\prime(t)\textbf{j} + z\prime(t)\textbf{k}\\&= 3 \textbf{i} + (12 + 4)\textbf{j} + (e^t\sin t + \cos t e^t )\textbf{k}\end{aligned}

This shows that finding the derivative of vector functions is straightforward. It is important to refresh on the fundamental derivative rules we’ve learned in the past since we’ll need them to simplify the expressions of the components. When you need to, review your notes on derivative rules – including the derivative rules for trigonometric functions.

We’ve prepared a set of problems for you to work and we hope that by the end of it, you’re more confident with your understanding of vector functions’ derivatives.

Example 1

Use the formal definition of derivative to differentiate the vector-valued function, $\textbf{r}(t) = (2t – 1)\textbf{i} + (t^2 – 2t + 1)\textbf{j}$.

Solution

Recall that we can define $\textbf{r}\prime(t)$ as shown below.

\begin{aligned}\textbf{r}\prime(t)&= \lim_{h \rightarrow 0} \dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}\end{aligned}

Let’s first simplify the expression for $\textbf{r}(t + h) – \textbf{r}(t)$.  Evaluate each component of $\textbf{r}$ at $(t + h)$.

\begin{aligned}\textbf{r}(t + h) &= [2(t + h) – 1]\textbf{i} + [(t + h)^2 – 2(t + h) + 1)]\textbf{j}\\&= (2t + 2h – 1)\textbf{i} + (t^2 + 2th + h^2 – 2t – 2h + 1)\textbf{j}\end{aligned}

Subtract the expression for $\textbf{r}(t)$ from the result to simplify the numerator, $\textbf{r}(t + h) – \textbf{r}$.

\begin{aligned}\textbf{r}(t + h) – \textbf{r}(t) &= [2(t + h) – 1]\textbf{i} + [(t + h)^2 – 2(t + h) + 1)]\textbf{j}\\&=[(2t + 2h – 1)\textbf{i} + (t^2 + 2th + h^2 – 2t – 2h + 1)\textbf{j}] \\&\phantom{xx}- [(2t -1)\textbf{i} + (t^2 – 2t + 1)\textbf{j}]\\&= [(2t + 2h – 1) – (2t – 1)]\textbf{i}\\&\phantom{xx}+[(t^2 + 2th + h^2 – 2t – 2h + 1) – (t^2 – 2t + 1)]\textbf{j}\\&= 2h \textbf{i} + (h^2 + 2th – 2h)\textbf{j}\end{aligned}

This means that we can write $\textbf{r}\prime(t)$ as shown below.

\begin{aligned}\textbf{r}\prime(t)&= \lim_{h \rightarrow 0} \dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}\\&= \lim_{h \rightarrow 0}\dfrac{2h \textbf{i} + (h^2 + 2th – 2h)\textbf{j}}{h}\\&= \lim_{h \rightarrow 0} \dfrac{h[2 \textbf{i} + (h + 2t -2)\textbf{j}]}{h} \\&= \lim_{h \rightarrow 0} 2 \textbf{i} + (h + 2t -2)\textbf{j}\\&= 2\textbf{i} + (2t -2)\textbf{j} \end{aligned}

This means that through the formal definition of derivatives, we have shown that $\textbf{r}\prime(t) = 2\textbf{i} + (2t -2)\textbf{j}$. We can actually confirm this by differentiating each component as well!

Example 2

Find the derivative of the following vector-valued functions.

a. $\textbf{r}(t) = (2t + 8)\textbf{i} + (2t^2 – 6t + 8) \textbf{j}$
b. $\textbf{r}(t) = \left<2\cos t, 6\sin t, 2\tan t\right>$
c. $\textbf{r}(t) = (t^2 -1)\textbf{i} + (e^t \cos t) \textbf{j} + (e^{3t}) \textbf{k}$

Solution

We can find the derivative of vector functions by differentiating each of its components. For the three items, we’ll work on the derivatives of the components to write the respective expressions for $\textbf{r}\prime(t)$.

For the first function, let’s find the derivatives of $(2t + 8)$ and $(2t^2 – 6t + 8)$. Use the resulting expressions for the components of $\textbf{r}\prime(t)$.

Write $\textbf{r}\prime(t)$ as $x\prime(t) \textbf{i} + y\prime(t) \textbf{j}$.

a. This means that $\textbf{r}\prime(t)$ is equal to $2 \textbf{i} + (4t – 6)\textbf{j}$.

Apply a similar process to find the derivative of the second vector function. Use the following derivative rules to simplify each expressions:

• $\dfrac{d}{dt} \cos t = -\sin t$
• $\dfrac{d}{dt} \sin t = \cos t$
• $\dfrac{d}{dt} \tan t = \sec^2 t$

b. From this, we can see that the derivative of the vector function is equal to $\left<-2 \sin t, 6 \cos t, 2\sec^2 t\right>$.

Let’s now work on the third vector-valued function, $\textbf{r}(t) = (t^2 -1)\textbf{i} + (e^t \cos t) \textbf{j} + (e^{3t}) \textbf{k}$.

Let’s use these resulting expressions to write down the expression for $\textbf{r}\prime(t) = x\prime(t) \textbf{i} + y\prime(t) \textbf{j} + y\prime(t) \textbf{k}$.

c. Hence, we have $\textbf{r}\prime(t) = 2t \textbf{i} + e^t(\cos t – \sin t)\textbf{j} + 3e^{3t}\textbf{k}$.

Example 3

\begin{aligned}\dfrac{d}{dt} \phantom{x}[k\textbf{u}(t)] &= k \textbf{u}\prime(t)\\ \dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \pm \textbf{v}(t) ] &= \textbf{u}\prime(t) \pm \textbf{v}\prime(t)\end{aligned}

Use the derivative properties shown above to prove the scalar product property of the vector-valued function: $\dfrac{d}{dt} [f(t)\textbf{v}(t)] = f\prime(t)\textbf{v}(t) + f(t)\textbf{v}\prime(t)$.

Solution

We can write $\textbf{v}(t)$ as $x(t) \textbf{i} + y(t) \textbf{j}$, so rewrite $\dfrac{d}{dt} [f(t)\textbf{v}(t)]$ as shown below.

\begin{aligned}\dfrac{d}{dt} [f(t)\textbf{v}(t)] &= \dfrac{d}{dt}\{f(t) [x(t) \textbf{i} + y(t) \textbf{j}]\}\\&= \dfrac{d}{dt}[f(t)x(t) \textbf{i} + f(t)y(t) \textbf{j}]\\&= \dfrac{d}{dt} f(t)x(t) \textbf{i} + \dfrac{d}{dt}f(t)y(t) \textbf{j},\phantom{x}\text{Sum Rule}\end{aligned}

Apply the product rule to expand the right-hand side of the equation. Group the terms that contain $f\prime(t)$ and $f(t)$.

\begin{aligned}\dfrac{d}{dt} [f(t)\textbf{v}(t)] &= \dfrac{d}{dt} f(t)x(t) \textbf{i} + \dfrac{d}{dt}f(t)y(t) \textbf{j}\\&= [f\prime(t)x(t) + f(t)x\prime(t)] \textbf{i} + [f\prime(t)y(t) + f(t)y\prime(t)] \textbf{j} \\&= f\prime(t)[x(t) \textbf{i} + y(t)\textbf{j}] + f(t)[x\prime(t) \textbf{i} + y\prime(t)\textbf{j}]\end{aligned}

Rewrite $x(t) \textbf{i} + y(t)\textbf{j}$ and $x\prime(t) \textbf{i} + y\prime(t)\textbf{j}$ as $\textbf{v}(t)$ and $\textbf{v}\prime(t)$, respectively.

\begin{aligned}\dfrac{d}{dt} [f(t)\textbf{v}(t)]&= f\prime(t)\textbf{v}(t) + f(t)\textbf{v}\prime(t)\end{aligned}

This confirms that the scalar product property remains true for vector-valued functions.

Example 4

Using the six other derivative properties, show that when $\textbf{u}(t) \cdot \textbf{u}(t) =c$ , then $\textbf{u}(t) \cdot \textbf{u}\prime(t) = 0$.

Solution

Using the dot product derivative rule, we have $\dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \cdot \textbf{v}(t)]  = \textbf{u}\prime(t) \cdot \textbf{v}(t) + \textbf{u}(t) \cdot \textbf{v}\prime(t)$.

\begin{aligned} \textbf{u}(t) \cdot \textbf{u}(t) &= c\\\dfrac{d}{dt} [\textbf{u}(t) \cdot \textbf{u}(t)] &= \dfrac{d}{dt} c\\\textbf{u}\prime(t) \cdot \textbf{u}(t) + \textbf{u}(t) \cdot \textbf{u}\prime(t) &= 0\end{aligned}

Simplify the right-hand side of the equation to further simplify the equation.

\begin{aligned} 2 [\textbf{u}(t) \cdot \textbf{u}\prime(t)] &= 0 \\\textbf{u}(t) \cdot \textbf{u}\prime(t) &= 0\end{aligned}

This confirms the seventh derivative property, $\textbf{u}(t) \cdot \textbf{u}\prime(t) = 0$.

Example 5

Suppose that we have the following vector functions:

\begin{aligned}\textbf{u}(t) &= (2t – 1) \textbf{i} + (2t^2 – 4t + 1)\textbf{j} +  6t\textbf{k} \\\textbf{v}(t) &= (t^2 – 4) \textbf{i} + (4t – 5)\textbf{j} +  (t^3 – 6t)\textbf{k} \end{aligned}

Calculate the following derivatives by applying key properties we’ve learned for vector-valued functions.

a. $\dfrac{d}{dt}[\textbf{u}(t) \cdot \textbf{v}(t)]$
b. $\dfrac{d}{dt}[\textbf{u}(t) \times \textbf{u}\prime(t)]$

Solution

Our vector-valued functions’ derivative properties will now come in handy with this example. Before we can apply the different formulas, we’ll need to know the expressions for $\textbf{u}\prime(t)$ and $\textbf{v}\prime(t)$. Let’s differentiate the two vector functions first by differentiating each of their components.

\begin{aligned}\textbf{u}\prime(t) &= \dfrac{d}{dt}(2t – 1) \textbf{i} + \dfrac{d}{dt}(2t^2 – 4t + 1)\textbf{j} +  \dfrac{d}{dt}6t\textbf{k}\\&=[2(1) – 0]\textbf{i} + [2(2t^{2 -1}) – 4(1) + 0]\textbf{j} + [6(1)]\textbf{k}\\&= 2\textbf{i} + (4t – 4)\textbf{j} + 6\textbf{k}\\\\\textbf{v}\prime(t) &= \dfrac{d}{dt}(t^2 – 4) \textbf{i} + \dfrac{d}{dt}(4t – 5)\textbf{j} +  \dfrac{d}{dt}(t^3 – 6t)\textbf{k}\\&=[(2t^{2 – 1}) – 0]\textbf{i} + [4(1) – 0]\textbf{j} + [(3t^{3 – 1}) – 6(1)]\textbf{k}\\&= 2t\textbf{i} + 4\textbf{j} + (3t^2 – 6)\textbf{k} \end{aligned}

For the first item, we’re dealing with the derivative of the dot product of $\textbf{u}(t)$ and $\textbf{v}(t)$, so we’ll use the dot product property shown below.

\begin{aligned} \dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \cdot \textbf{v}(t)]  = \textbf{u}\prime(t) \cdot \textbf{v}(t) + \textbf{u}(t) \cdot \textbf{v}\prime(t) \end{aligned}

Substitute the expressions for $\textbf{u}(t)$, $\textbf{v}(t)$, $\textbf{u}\prime(t)$, and $\textbf{v}\prime(t)$.

\begin{aligned} \dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \cdot \textbf{v}(t)]  &= \textbf{u}\prime(t) \cdot \textbf{v}(t) + \textbf{u}(t) \cdot \textbf{v}\prime(t)\\&= [2\textbf{i} + (4t – 4)\textbf{j} + 6\textbf{k}] \cdot [(t^2 – 4) \textbf{i} + (4t – 5)\textbf{j} +  (t^3 – 6t)\textbf{k}]\\&\phantom{xx}+ [(2t – 1) \textbf{i} + (2t^2 – 4t + 1)\textbf{j} +  6t\textbf{k} ] \cdot [2t\textbf{i} + 4\textbf{j} + (3t^2 – 6)\textbf{k} ] \end{aligned}

Simplify the expressions for $\textbf{u}\prime(t) \cdot \textbf{v}(t)$ and $\textbf{u}(t) \cdot \textbf{v}\prime(t)$.

\begin{aligned} \dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \cdot \textbf{v}(t)]  &= [2(t^2 -4) \textbf{i}\cdot \textbf{i}+ (4t – 4)(4t – 5)\textbf{j}\cdot \textbf{j} + 6(t^3 – 6t)\textbf{k}\cdot \textbf{k} ]\\&\phantom{xx}+ [(2t -1)(2t)\textbf{i}\cdot \textbf{i} + (2t^2 – 4t + 1)(4)\textbf{j}\cdot \textbf{j} + 6t(3t^2 – 6) \textbf{k}\cdot \textbf{k}]\\ &=  [(2t^2 – 8) +(16t^2 -36t + 20) + (6t^3 – 36t) ]\\&\phantom{xx} + [(4t^2 – 2t) +(8t^2 – 16t + 4) + (18t^3 – 36t) ]\\&= 24t^3 + 30t^2- 126t +16\end{aligned}

a. This means that $\dfrac{d}{dt}[\textbf{u}(t) \cdot \textbf{v}(t)] = 24t^3 + 30t^2- 126t +16$.

Now, let’s evaluate the derivative of the vector functions’ cross product using the fifth property from the table of properties we’ve shown. This means that we have
\begin{aligned}\dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \times \textbf{u}\prime(t)] &= \textbf{u}\prime(t) \times \textbf{u}\prime(t) + \textbf{u}(t) \times \textbf{u}\prime\prime(t)\end{aligned}
Recall that the cross-product of the vector with itself is equal to zero, so we can simplify the expression as shown below.
\begin{aligned}\dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \times \textbf{u}\prime(t)] &= 0+ \textbf{u}(t) \times \textbf{u}\prime\prime(t)\\&= \textbf{u}(t) \times \textbf{u}\prime\prime(t)\end{aligned}
To find the expression of $\textbf{u}\prime\prime(t)$, differentiate the components of $\textbf{u}\prime(t)$.
\begin{aligned} \textbf{u}\prime\prime(t) &= \dfrac{d}{dt}[\textbf{u}\prime(t)]\\&= \dfrac{d}{dt}[2\textbf{i} + (4t – 4)\textbf{j} + 6\textbf{k}]\\&= \dfrac{d}{dt}2\textbf{i} + \dfrac{d}{dt}(4t – 4)\textbf{j} + \dfrac{d}{dt}6\textbf{k}\\&= 0 \textbf{i} + 4 \textbf{j} + 0 \textbf{k}\end{aligned}
Let’s go back to our previous expression and find the cross-product between $\textbf{u}(t)$ and $\textbf{u}\prime\prime(t)$.
\begin{aligned}\dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \times \textbf{u}\prime(t)] &=[(2t – 1) \textbf{i} + (2t^2 – 4t + 1)\textbf{j} + 6t\textbf{k} ]\times [ 0 \textbf{i} + 4 \textbf{j} + 0 \textbf{k}]\\&= [\left(2t^2-4t+1\right)\cdot \:0-6t\cdot \:4]\textbf{i} + [6t\cdot \:0-\left(2t-1\right)\cdot \:0]\textbf{j} + [4-\left(2t^2-4t+1\right)\cdot \:0]\textbf{k}\\&= -24t\textbf{i} + 4(2t -1)\textbf{k}\end{aligned}

b. Hence, $\dfrac{d}{dt}[\textbf{u}(t) \times \textbf{u}\prime(t)]$ is equivalent to $-24t\textbf{i} + 4(2t -1)\textbf{k}$.

Example 6

Determine the unit tangent vector for the following vector functions:

a. $\textbf{u}(t) = \sin t \textbf{i} + \cos t \textbf{j}$
b. $\textbf{v}(t) = (4t +2)\textbf{i} + (1 -t^2)\textbf{j} + (2t + 3)\textbf{k}$

Solution

We can find the unit tangent vector using the formula shown below.

\begin{aligned}\textbf{T}(t) &= \dfrac{\textbf{r}\prime(t)}{|\textbf{r}\prime(t)|}\end{aligned}

This means that we’ll need to find the derivative of the vector function then divide the result by the magnitude of the vector’s derivative.

For the case of $\textbf{u}(t) = \sin t \textbf{i} + \cos t \textbf{j}$, we’ll differentiate each component to find the expression for $\textbf{u}\prime(t)$.

\begin{aligned}\textbf{u}\prime(t) &= \dfrac{d}{dt}(\sin t) \textbf{i} + \dfrac{d}{dt}(\cos t )\textbf{j} \\&= (\cos t) \textbf{i} – (\sin t)\textbf{j}\end{aligned}

Now, to find the expression for $|\textbf{u}\prime(t)|$, add the squares of the components then take the square root of the sum.

\begin{aligned}|\textbf{u}\prime(t)| &= \sqrt{(\cos t)^2 + [- (\sin t)]^2 }\\&= \sqrt{\cos^2 t + \sin^2 t}\\&= \sqrt{1}\\&= 1\end{aligned}

The unit tangent vector of $\textbf{u}(t)$ is simply equal to $\textbf{T}(t) = \dfrac{\textbf{u}\prime(t)}{\sqrt{\textbf{u}\prime(t)}}$.Hence, we have the following:

\begin{aligned}\textbf{T}(t) &= \dfrac{\textbf{u}\prime(t)}{|\textbf{u}\prime(t)|}\\&=\dfrac{(\cos t) \textbf{i} – (\sin t)\textbf{j}}{1} \\&= (\cos t) \textbf{i} – (\sin t)\textbf{j}\end{aligned}

a. This means that the vector function, $\textbf{u}(t) = \sin t \textbf{i} + \cos t \textbf{j}$, has a unit vector at $\textbf{T}(t) f= (\cos t) \textbf{i} – (\sin t)\textbf{j}$.

Apply a similar process to find the unit tangent vector of $\textbf{v}(t)$. We begin by finding the derivative of the vector-valued function.

\begin{aligned}\textbf{v}\prime(t) &= \dfrac{d}{dt}(4t +2)\textbf{i} + \dfrac{d}{dt}(1 -t^2)\textbf{j} + \dfrac{d}{dt}(2t + 3)\textbf{k}\\&= [4(1) + 0] \textbf{i} + [0- 2(t^{2 – 1})] \textbf{j} +[2(1) + 0] \textbf{k}\\&= 4 \textbf{i} – 2t \textbf{j} + 2 \textbf{k}\end{aligned}

Let’s now find the expression for $|\textbf{v}\prime(t)|$ by adding the square of each component then taking the square root of the expression.

\begin{aligned}|\textbf{v}\prime(t)| &= \sqrt{(4)^2 + (-2t)^2 + (2)^2}\\&= \sqrt{4t^2 + 20}\\&= \sqrt{4(t^2 + 5)}\\&= 2\sqrt{t^2 + 5}\end{aligned}

Find the unit tangent vector by dividing each component of $\textbf{v}\prime(t)$ by its magnitude.

\begin{aligned}\textbf{T}(t) &= \dfrac{\textbf{v}\prime(t)}{|\textbf{v}\prime(t)|}\\&=\dfrac{4 \textbf{i} – 2t \textbf{j} + 2 \textbf{k}}{2\sqrt{t^2 + 5}} \\&= \dfrac{4}{2\sqrt{t^2 + 5}} \textbf{i} –  \dfrac{2t}{2\sqrt{t^2 + 5}}\textbf{j} + \dfrac{2}{2\sqrt{t^2 + 5}} \textbf{k}\\&=  \dfrac{2}{\sqrt{t^2 + 5}} \textbf{i} –  \dfrac{t}{\sqrt{t^2 + 5}}\textbf{j} + \dfrac{1}{\sqrt{t^2 + 5}} \textbf{k}\end{aligned}

b. Hence, the unit tangent vector of $\textbf{v}(t)$ is equal to $\dfrac{2}{\sqrt{t^2 + 5}} \textbf{i} – \dfrac{t}{\sqrt{t^2 + 5}}\textbf{j} + \dfrac{1}{\sqrt{t^2 + 5}} \textbf{k}$.

Example 7

What is the equation of the line that is tangent to the curve, $\textbf{r}(t) = \left<2t^2, 1- t^2, t^3\right>$, at $t = 2$?

Solution

The equation of the line that is tangent to the vector, $\textbf{r}(t)$, can be expressed as $\textbf{L} = \textbf{r}(t_o) + t\textbf{r}\prime(t_o)$. To find the equation of the line, let’s first take the derivative of $\textbf{r}(t)$.

\begin{aligned}\textbf{r}\prime(t) &= \left<\dfrac{d}{dt} 2t^2, \dfrac{d}{dt} 1- t^2, \dfrac{d}{dt} t^3\right>\\&= \left<2(2t^{2-1}), (0 – 2t^{2 -1}), 3t^{3- 1}\right>\\&= \left<4t, -2t, 3t^2\right>\end{aligned}

Evaluate $\textbf{r}(t)$ and $\textbf{r}\prime(t)$ at $t = 2$ then substitute these values into the equation of the line: $\textbf{L} = \textbf{r}(2) + t\textbf{r}\prime(2)$.

This means that the equation of the line that is tangent to the curve of $\textbf{r}(t)$ and passes through $t = 2$ is equal to $\textbf{L} = \left<8 + 8t, -3 – 4t, 8 + 12t\right>$.

Practice Questions

1. Use the formal definition of derivative to differentiate the vector-valued function, $\textbf{r}(t) = (3t– 1)\textbf{i} + (t^2 – 4t + 3)\textbf{j}$.

2. Find the derivative of the following vector-valued functions.
a. $\textbf{r}(t) = (4t + 8)\textbf{i} + (3t^3 – 4t^2 – 8t) \textbf{j}$
b. $\textbf{r}(t) = <8\cos t, \sin 12t, 2\sec t>$
c. $\textbf{r}(t) = \sqrt{t -1}\textbf{i} + (e^{2t} \sin t) \textbf{j} + (te^{5t}) \textbf{k}$

3. Use the derivative properties to prove the dot product property of vector functions: $\dfrac{d}{dt}\phantom{x} [\textbf{u}(t) \cdot \textbf{v}(t)] = \textbf{u}\prime(t) \cdot \textbf{v}(t) + \textbf{u}(t) \cdot \textbf{v}\prime(t)$.

4. Suppose that we have the following vector functions:
\begin{aligned}\textbf{u}(t) &= (4t – 4) \textbf{i} + (3t^2 – 6t + 8)\textbf{j} + 4t\textbf{k} \\\textbf{v}(t) &= (-2t^2 – 8) \textbf{i} + (12t – 8)\textbf{j} + (t^4 – 12t^2)\textbf{k} \end{aligned}

Calculate the following derivatives by applying key properties we’ve learned for vector-valued functions.
a. $\dfrac{d}{dt}[\textbf{u}(t) \cdot \textbf{v}(t)]$
b. $\dfrac{d}{dt}[\textbf{u}(t) \times \textbf{u}\prime(t)]$
c. $\dfrac{d}{dt}[\textbf{v}(t) \times \textbf{v}\prime(t)]$

5. Determine the unit tangent vector for the following vector functions:
a. $\textbf{u}(t) = 4\sin t \textbf{i} + 4 \cos t \textbf{j}$
b. $\textbf{v}(t) = (t^2 + 4)\textbf{i} + (3t – 4)\textbf{j} + \ln(4t) \textbf{k}$
6. What is the equation of the line that is tangent to the curve, $\textbf{r}(t) = \left<4t^2, 1- 3t^3, 2t^4\right>$, at $t = 1$?

Answer Key

1.
$ \begin{aligned}\textbf{r}\prime(t)&= \lim_{h \rightarrow 0} \dfrac{\textbf{r}(t + h) – \textbf{r}(t)}{h}\\&= \lim_{h \rightarrow 0}\dfrac{3h \textbf{i} + (h^2 + 2th – 4h)\textbf{j}}{h}\\&= \lim_{h \rightarrow 0} \dfrac{h[3 \textbf{i} + (h + 2t – 4)\textbf{j}]}{h} \\&= \lim_{h \rightarrow 0} 3 \textbf{i} + (h + 2t – 4)\textbf{j}\\&= 3\textbf{i} + (2t -4)\textbf{j} \end{aligned}$
2.
a. $\textbf{r}\prime(t) = 4\textbf{i} + (9t^2 – 8t – 8) \textbf{j}$
b. $\textbf{r}\prime(t) = \left<-8\sin t, 12\cos 12t, 2\sec t \tan t\right>$
c. $\textbf{r}\prime(t) = \dfrac{1}{2\sqrt{t -1}}\textbf{i} + e^{2t} (2\sin t + \cos t) \textbf{j} + e^{5t}(t + 1) \textbf{k}$
3.
$\begin{aligned}\textbf{u}(t) &= f_1(t) \textbf{i} + g_1(t) \textbf{j}\\\textbf{v}(t) &= f_2(t) \textbf{i} + g_2(t) \textbf{j}\\\textbf{u}(t) \cdot \textbf{v}(t) &= f_1(t)f_2(t) + g_1(t)g_2(t)\\\\\dfrac{d}{dt}[\textbf{u}(t) \cdot \textbf{v}(t)]&= \dfrac{d}{dt}[f_1(t)f_2(t) + g_1(t)g_2(t)]\\&= \dfrac{d}{dt}[f_1(t)f_2(t)] + \dfrac{d}{dt}[g_1(t)g_2(t)]\\&= f_1\prime(t)f_2(t)+ g_1\prime(t)g_2(t) +f_1(t)f_2′(t)+ g_1(t)g_2\prime(t)\\&= [f_1\prime(t) + g_1\prime(t)]\textbf{i} \cdot [f_2(t) + g_2(t)]\textbf{j}\\&\phantom{xx}+ [f_1(t) + g_1(t)]\textbf{i} \cdot [f_2\prime(t) + g_2\prime(t)]\textbf{j}\\&= \textbf{u}\prime(t) \cdot \textbf{v}(t)+ \textbf{u}(t) \cdot \textbf{v}\prime(t)\end{aligned}$
4.
a. $\dfrac{d}{dt}[\textbf{u}(t) \cdot \textbf{v}(t)] = 20t^4 -60t^2 -176t + 112$
b. $\dfrac{d}{dt}[\textbf{u}(t) \times \textbf{u}\prime(t)] = (-12t^2 + 32) \textbf{i} + 16\textbf{j} + (12t^2 – 24t – 8)\textbf{k}$
c. $\dfrac{d}{dt}[\textbf{v}(t) \times \textbf{v}\prime(t)] = (36t^4 – 32t^3 – 144t^2 +192t) \textbf{i} + (4t^5 +32t^3 -192t)\textbf{j} + (24t^2 – 32t – 96)\textbf{k}$
5.
a. $\textbf{T}(t) = \cos t \textbf{i} – \sin t \textbf{j}$
b. $\textbf{T}(t) = \dfrac{2t^2}{\sqrt{4t^4 + 9t^2 + 1}} \textbf{i} + \dfrac{9t}{\sqrt{4t^4 + 9t^2 + 1}} \textbf{j} + \dfrac{1}{\sqrt{4t^4 + 9t^2 + 1}} \textbf{k}$
6. The equation of the line tangent to the vector is $\textbf{L}(t) =\left<4+ 8t, -2 – 9t, 2 + 8t\right>$.