Cramer’s Rule – Explanation & Examples
To solve a system of equations, we primarily use the substitution method, elimination method, or graphing method. We can also use matrix algebra to solve a system of equations. Processes such as Gaussian Elimination (also known as Gauss-Jordan Elimination) can help solve a system of equations with $ 3 $ or more unknowns. We can also use Cramer’s Rule to solve a system.
What is the Cramer’s Rule?
The Cramer’s Rule is a method of solving a system of equations using determinants.
In this lesson, we will look at what the Cramer’s Rule is and how to solve a system of equations. Some examples and practice problems will follow.
What is Cramer’s Rule?
The Cramer’s Rule is a method to solve a system of equations using determinants. That’s that beauty of the Cramer’s Rule. We can find a single variable’s value without solving the whole system (or other variables).
Remember determinants?
Consider the $ 2 \times 2 $ matrix shown below:
$ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $
The determinant of this matrix is given by:
$ det( A ) = | A | = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad – bc $
Note: We have used $ 3 $ notations in denoting a determinant.
Now, consider the $ 3 \times 3 $ matrix shown below:
$ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $
The determinant of this matrix is given by:
$ det( B ) = | B | = \begin{vmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {vmatrix} = a \begin{vmatrix} { e } & f \\ h & i \end {vmatrix} – b \begin{vmatrix} d & f \\ g & i \end {vmatrix} + c \begin{vmatrix} d & e \\ g & h \end {vmatrix} $
Note that we have broken down the $3\times 3$ matrix into smaller $2\times 2$ matrices. The vertical bars outside the $ 2 \times 2 $ matrices indicate that we have to take the determinant. From knowledge of determinant of $ 2 \times 2 $ matrices, we can further simplify the formula to be:
$ det(B)=| B | = a(ei-fh) – b(di – fg) + c(dh-eg) $
Let’s consider a system of equations shown below:
$ \begin{align*} { 2x } + 3y &= \, { 7 } \\ { – 3x } + 4y &= { 15 } \end{align*} $
We will now name some matrices to help us out with using the Cramer’s Rule to solve this system later on.
- Following the $ 2 \times 2 $ determinant formula, we can write the determinant matrix as:
$ D = \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix} $
We labeled it “D.”
- Putting the constant coefficients from the system in the first column (in place of $ x $s), we can write another matrix:
$ D_{ x } = \begin{vmatrix} 7 & 3 \\ { 15 } & 4 \end{vmatrix} $
We labeled it “$ D_{ x } $” and call it the x-matrix.
- Similarly, putting the constants from the system in the second column (in place of $ y $s), we can write another matrix:
$ D_{ y } = \begin{vmatrix} 2 & 7 \\ { – 3 } & 15 \end{vmatrix} $
We labeled it “$ D_{ y } $” and call it the y-matrix.
Now, the formula of Cramer’s Rule to solve for the variables $ x $ and $ y $ are shown below:
$ x = \frac{ D_{ x } }{ D } = \frac{ \begin{vmatrix} 7 & 3 \\ { 15 } & 4 \end{vmatrix} }{ \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix} } $
$ y = \frac{ D_{ y } }{ D } = \frac{ \begin{vmatrix} 2 & 7 \\ { – 3 } & 15 \end{vmatrix} }{ \begin{vmatrix} 2 & 3 \\ { – 3 } & 4 \end{vmatrix} } $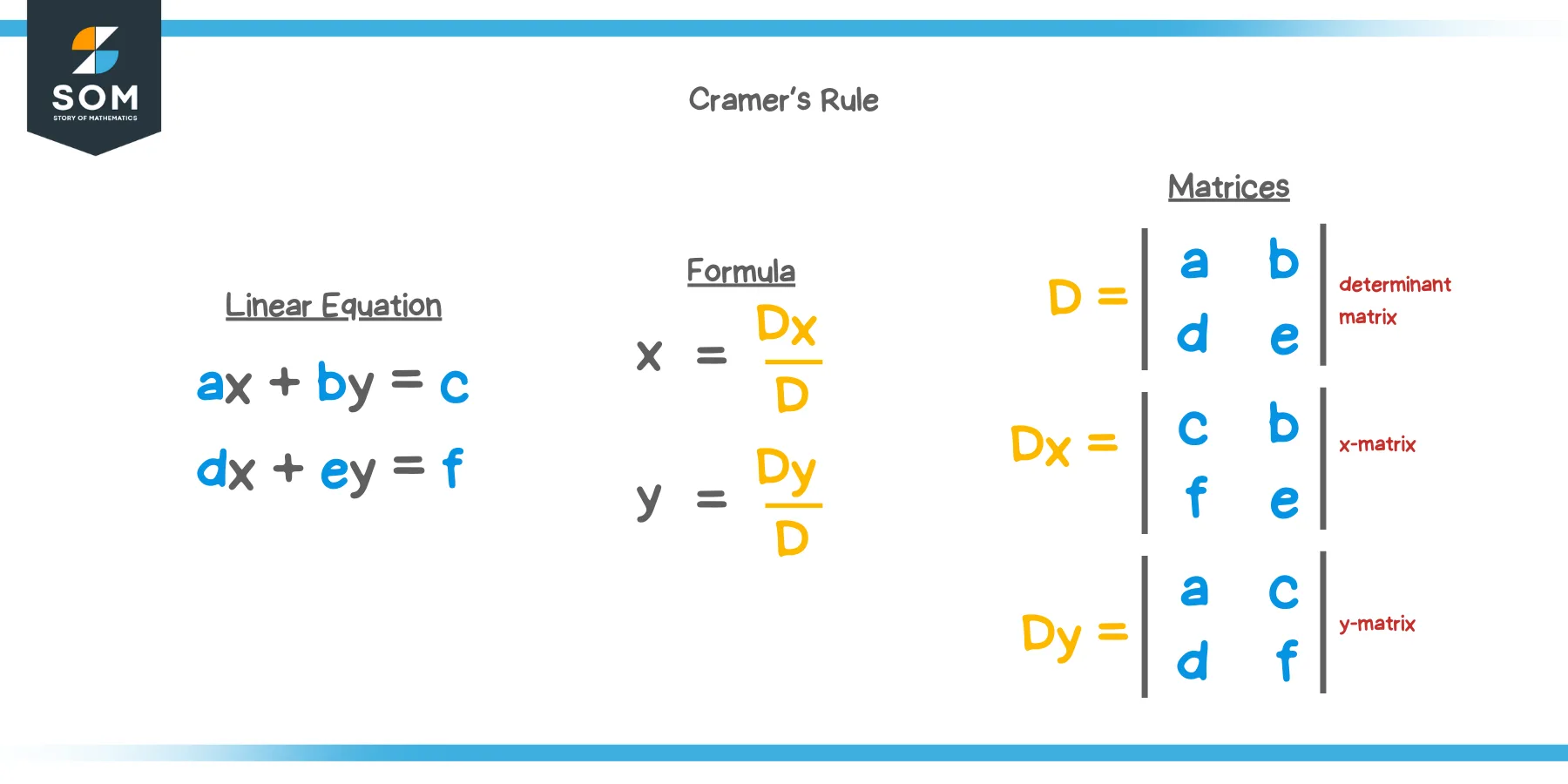
The next section will show us how to actually use the rule and solve the system! Note that we cannot use the Cramer’s Rule when a matrix’s determinant is $ 0 $! Zero determinant can mean:
- The system is inconsistent (it doesn’t have a solution)
- The system is dependent (it has infinite solutions)
In this case, we have to rely upon other methods in solving a system, such as the substitution/elimination method or Gaussian Elimination method.
How to use Cramer’s Rule?
Let’s solve a system of equations ( $ 2 $ variables ) using the Cramer’s Rule to see the concept live in action!
Solve the system of equations shown below using the Cramer’s Rule:
$ \begin{align*} { 2x } + y &= \, { 7 } \\ { 3x } – 2y &= { – 7 } \end{align*} $
The first step is to write the determinants of this system of equations, determinant ( $ D $ ), $ x – $ determinant ( $ D_{ x } ), and the $ y – $ determinant ( $ D_{ y } ). Let’s use the formula we learned and write them up:
$ D = \begin{vmatrix} 2 & 1 \\ { 3 } & { – 2 } \end{vmatrix} $
$ D_{ x } = \begin{vmatrix} 7 & 1 \\ { – 7 } & { – 2 } \end{vmatrix} $
$ D_{ y } = \begin{vmatrix} 2 & { 7 } \\ { 3 } & { – 7 } \end{vmatrix} $
Recall the formula to evaluate a $ 2 \times 2 $ determinant:
For a $ 2 \timess 2 $ matrix —
$ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} $
The determinant is calculated as —
$ det( A ) = | A | = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad – bc $
Let’s calculate the determinants:
$ D = \begin{vmatrix} 2 & 1 \\ { 3 } & { – 2 } \end{vmatrix} = ( 2 )( – 2 ) – ( 1 )( 3 ) = – 4 – 3 = – 7 $
$ D_{ x } = \begin{vmatrix} 7 & 1 \\ { – 7 } & { – 2 } \end{vmatrix} = ( 7 )( – 2 ) – ( 1 )( – 7 ) = – 14 – ( – 7 ) = – 14 + 7 = – 7 $
$ D_{ y } = \begin{vmatrix} 2 & { 7 } \\ { 3 } & { – 7 } \end{vmatrix} = ( 2 )( – 7 ) – ( 7 )( 3 ) = -14 – 21 = – 35 $
Now, we can use the formulas and thus, the Cramer’s Rule, to solve for the variables $ x $ and $ y $. Shown below:
$ x = \frac{ D_{ x } }{ D } = \frac{ – 7 }{ – 7 } = 1 $
$ y = \frac{D_{ y } }{ D } = \frac{ – 35 }{ – 7 } = 5 $
The solution set of the system is (1, 5).
You can notice that if we wanted to solve for only $ 1 $ variables without solving the whole system, we could have easily used the formula for a single variable to find it. Cramer’s Rule is a pretty nifty tool to use to find solutions to a system of equations. We will see some examples as well as one with $ 3 $ variables.
Example 1
Solve the system of equations shown below using Cramer’s Rule:
$ \begin{align*} { – x } – y &= \, { 5 } \\ { 2x } + y &= { 4 } \end{align*} $
Solution
The first step is to write the determinants of this system of equations, determinant ( $ D $ ), $ x – $ determinant ( $ D_{ x } ), and the $ y – $ determinant ( $ D_{ y } ). Let’s use the formula we learned and write them up:
$ D = \begin{vmatrix} – 1 & – 1 \\ { 2 } & { 1 } \end{vmatrix} $
$ D_{ x } = \begin{vmatrix} 5 & – 1 \\ { 4 } & { 1 } \end{vmatrix} $
$ D_{ y } = \begin{vmatrix} – 1 & { 5 } \\ { 2 } & { 4 } \end{vmatrix} $
We will use the formula to calculate the determinants of $ 2 \times 2 $ matrices to calculate the matrices $ D $, $ D_{ x } $, and $ D_{ y } $.
$ D = \begin{vmatrix} – 1 & – 1 \\ { 2 } & { 1 } \end{vmatrix} = ( – 1 )( 1 ) – ( – 1 )( 2 ) = – 1 + 2 = 1 $
$ D_{ x } = \begin{vmatrix} 5 & – 1 \\ { 4 } & { 1 } \end{vmatrix} = ( 5 )( 1 ) – ( – 1 )( 4 ) = 5 + 4 = 9 $
$ D_{ y } = \begin{vmatrix} – 1 & { 5 } \\ { 2 } & { 4 } \end{vmatrix} = ( – 1 )( 4 ) – ( 5 )( 2 ) = – 4 – 10 = – 14 $
Now, we use the formulas learned in Cramer’s Rule to find the values of the variables:
$ x = \frac{ D_{ x } }{ D } = \frac{ 9 }{ 1 } = 9 $
$ y = \frac{D_{ y } }{ D } = \frac{ – 14 }{ 1 } = – 14 $
The solution set of the system is $ (9, – 14) $.
Let us look at an example with $ 3 $ variables.
Example 2
Solve the system of equations shown below using Cramer’s Rule:
$ \begin{align*} 2a + b – 2c &= \, – 1 \\ 3a – 3b – c &= 5 \\ a – 2b + 3c = 6 \end{align*} $
Solution
The first step is to write the determinants of this system of equations, determinant ( $ D $ ), $ a – $ determinant ( $ D_{ a } ), $ b – $ determinant ( $ D_{ b } ), and the $ c – $ determinant ( $ D_{ c } ). Let’s use the formula we learned and write them up:
$ D = \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} $
$ D_{ a } = \begin{vmatrix} -1 & 1 & -2 \\ 5 & -3 & -1 \\ 6 & -2 & 3 \end{vmatrix} $
$ D_{ b } = \begin{vmatrix} 2 & -1 & -2 \\ 3 & 5 & -1 \\ 1 & 6 & 3 \end{vmatrix} $
$ D_{ c } = \begin{vmatrix} 2 & 1 & -1 \\ 3 & -3 & 5 \\ 1 & -2 & 6 \end{vmatrix} $
For a matrix in the form:
$ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $
The determinant is calculated as:
$ | B | = a(ei-fh) – b(di – fg) + c(dh-eg) $
Now, we use the Cramer’s Rule and calculate the values of the variables $ a $, $b$, and $c$. The steps are shown below (we didn’t show the detailed steps of finding determinants of $ 3 \times 3 $ matrices):
$ a = \frac{ D_{ a } }{ D } = \frac{ \begin{vmatrix} -1 & 1 & -2 \\ 5 & -3 & -1 \\ 6 & -2 & 3 \end{vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{-26}{-26} =1 $
$ b = \frac{D_{ b } }{ D } = \frac{ \begin{vmatrix} 2 & -1 & -2 \\ 3 & 5 & -1 \\ 1 & 6 & 3 \end{vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{26}{-26} = -1 $
$ c = \frac{D_{ c } }{ D } = \frac{ \begin{vmatrix} 2 & 1 & -1 \\ 3 & -3 & 5 \\ 1 & -2 & 6 \end{vmatrix} }{ \begin{vmatrix} 2 & 1 & -2 \\ 3 & -3 & -1 \\ 1 & -2 & 3 \end{vmatrix} } = \frac{-26}{-26} = 1$
The solution set of the system is $ (1, – 1,1) $.
Practice Questions
Solve the system of equations shown below using Cramer’s Rule:
$ \begin{align*} { 5x } + 2y &= \, { 10 } \\ { – x } + 4y &= { 20 } \end{align*} $
Solve the system of equations shown below using Cramer’s Rule:
$ \begin{align*} 3x – 4y + z &= \, -5 \\ x – y – z &= – 10 \\ 6x – 8y + 2z = 10 \end{align*} $
Answers
The first step is to write the determinants of this system of equations, determinant ( $ D $ ), $ x – $ determinant ( $ D_{ x } $ ), and the $ y – $ determinant ( $ D_{ y } $ ). Let’s use the formula we learned and write them up:
$ D = \begin{vmatrix} 5 & 2 \\ { – 1 } & { 4 } \end{vmatrix} $
$ D_{ x } = \begin{vmatrix} 10 & 2 \\ { 20 } & { 4 } \end{vmatrix} $
$ D_{ y } = \begin{vmatrix} 5 & { 10 } \\ { – 1 } & { 20 } \end{vmatrix} $
We will use the formula to calculate the determinants of $ 2 \times 2 $ matrices to calculate the matrices $ D $, $ D_{ x } $, and $ D_{ y } $.
$ D = \begin{vmatrix} 5 & 2 \\ { – 1 } & { 4 } \end{vmatrix} = ( 5 )( 4 ) – ( 2 )( -1 ) = 20 + 2 = 22 $
$ D_{ x } = \begin{vmatrix} 10 & 2 \\ { 20 } & { 4 } \end{vmatrix} = ( 10 )( 4 ) – ( 2 )( 20 ) = 40 – 40 = 0 $
$ D_{ y } = \begin{vmatrix} 5 & { 10 } \\ { – 1 } & { 20 } \end{vmatrix} = ( 5 )( 20 ) – ( 10 )( -1 ) = 100 + 10 = 110 $
Now, we use the formulas learned in Cramer’s Rule to find the values of the variables:
$ x = \frac{ D_{ x } }{ D } = \frac{ 0 }{ 22 } = 0 $
$ y = \frac{D_{ y } }{ D } = \frac{ 110 }{ 22 } = 5 $
The solution set of the system is $ (0, 5) $.
The first step is to write the determinants of this system of equations, determinant ( $ D $ ), $ x – $ determinant ( $ D_{ x } ), $ y – $ determinant ( $ D_{ y } ) $, and the $ z – $ determinant ( $ D_{ z } ) $. Let’s use the formula we learned and write them up:
$ D = \begin{vmatrix} 3 & -4 & 1 \\ 1 & -1 & -1 \\ 6 & -8 & 2 \end{vmatrix} $
$ D_{ x } = \begin{vmatrix} 5 & -4 & 1 \\ -10 & -1 & -1 \\ 10 & -8 & 2 \end{vmatrix} $
$ D_{ y } = \begin{vmatrix} 3 & 5 & 1 \\ 1 & -10 & -1 \\ 6 & 10 & 2 \end{vmatrix} $
$ D_{ z } = \begin{vmatrix} 3 & -4 & 5 \\ 1 & -1 & -10 \\ 6 & -8 & 10 \end{vmatrix} $
Recall that a $ 3 \times 3 $ matrix of the form:
$ B = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $
Has a determinant equals to:
$ | B | = a(ei-fh) – b(di – fg) + c(dh-eg) $
First, let’s find the value of the determinant, $D$,
$ D = \begin{vmatrix} 3 & -4 & 1 \\ 1 & -1 & -1 \\ 6 & -8 & 2 \end{vmatrix} = 3(-2-8) +4(2+6) +1(-8+6) = 3(-10) + 4(8) +1(-2) = 0 $
This matrix’s determinant is $ 0 $; thus, we cannot solve the system using Cramer’s Rule!!