JUMP TO TOPIC

Within the realm of geometry, a remarkable principle known as Corresponding Parts of Congruent Triangles is Congruent (CPCTC) unveils a hidden symmetry at the heart of triangle congruence.
CPCTC is a powerful tool, illuminating the profound relationship between congruent triangles and their corresponding parts. By establishing that corresponding sides, angles, and other elements of congruent triangles are themselves congruent, CPCTC enables geometric reasoning and proof construction with elegance and precision.
In this article, we delve into the depths of CPCTC, unraveling its underlying principles, exploring its practical applications, and demonstrating how this powerful concept unlocks many geometric insights.
Definition of CPCTC
The Corresponding Parts of Congruent Triangles are Congruent (CPCTC) is a fundamental principle in geometry that states that if two triangles are congruent, their corresponding parts (sides, angles, and other elements) are also congruent.
In other words, when two triangles are proven to be congruent through methods such as Side-Angle-Side (SAS), Side-Side-Side (SSS), or Angle-Side-Angle (ASA), the corresponding parts of these congruent triangles can be considered identical in terms of their measures or lengths.
This principle allows for applying congruence relationships to individual parts of triangles and facilitates geometric proofs and deductions. CPCTC is a powerful tool for establishing relationships and making conclusions about congruent triangles and their corresponding elements, contributing to the precision and rigor of geometric reasoning.
Below is the figure-1. We present a generic representation of CPCTC.
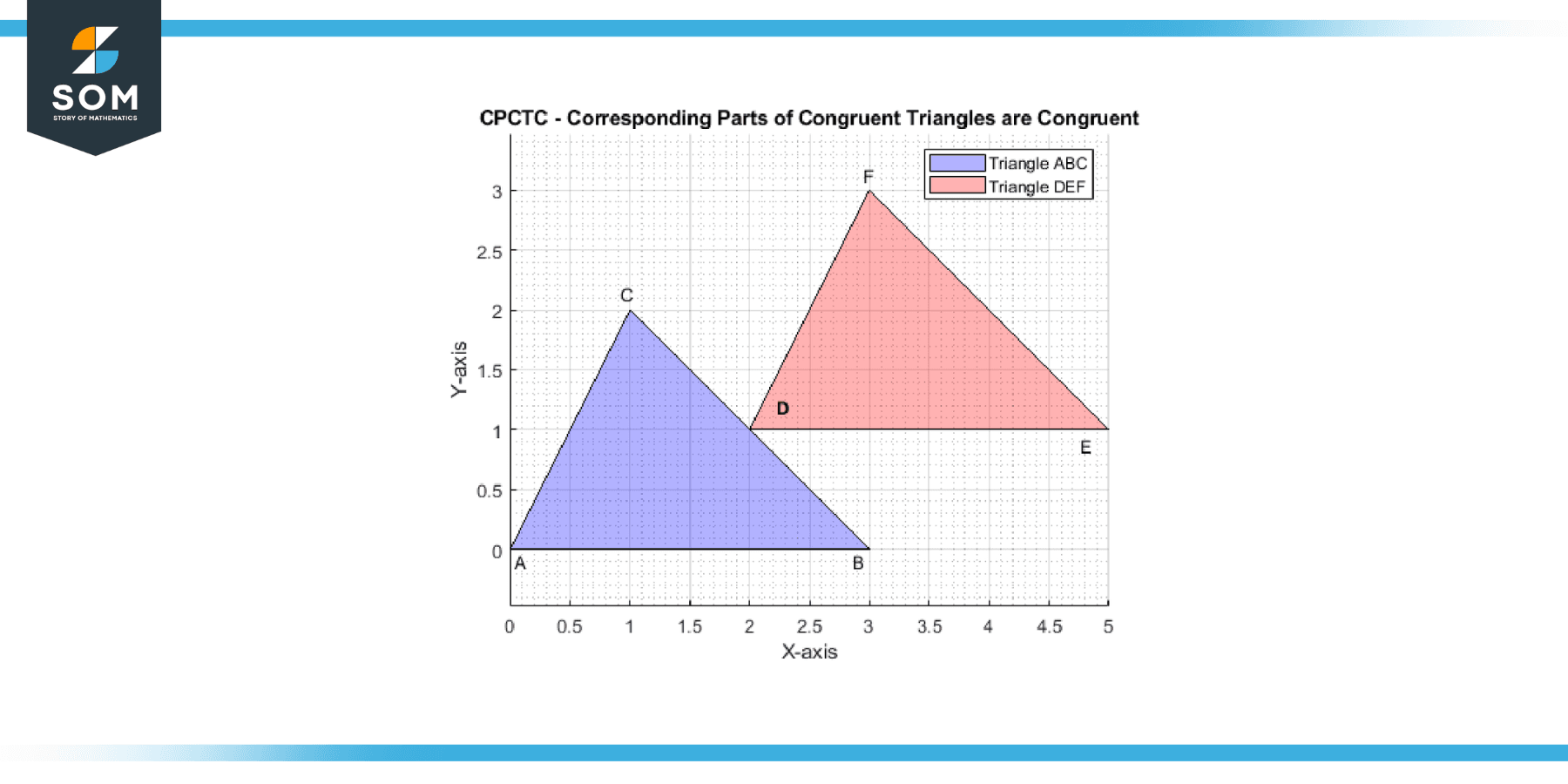
Figure-1.
Proof of CPCTC
The proof of CPCTC (Corresponding Parts of Congruent Triangles are Congruent) relies on the establishment of triangle congruence using one of several congruence criteria, such as Side-Angle-Side (SAS), Side-Side-Side (SSS), or Angle-Side-Angle (ASA). Let’s explore the proof of CPCTC in detail:
Proof of CPCTC:
- Given that triangle, ABC is congruent to triangle DEF (proven using a congruence criterion such as SAS, SSS, or ASA).
- We want to prove: Corresponding parts of congruent triangles are congruent.
- CPCTC states that congruent triangles’ corresponding sides, angles, and other elements are congruent.
- Let’s consider the corresponding sides of the congruent triangles:
- Side AB corresponds to side DE.
- Side BC corresponds to side EF.
- Side AC corresponds to side DF.
- By the congruence of triangles ABC and DEF, we know that the corresponding sides are congruent:
- AB ≅ DE
- BC ≅ EF
- AC ≅ DF
- Now, let’s consider the corresponding angles of the congruent triangles:
- Angle A corresponds to angle D.
- Angle B corresponds to angle E.
- Angle C corresponds to angle F.
- By the congruence of triangles ABC and DEF, we know that the corresponding angles are congruent:
- ∠A ≅ ∠D
- ∠B ≅ ∠E
- ∠C ≅ ∠F
- Therefore, we have established that the corresponding sides and angles of congruent triangles ABC and DEF are congruent.
- Other corresponding elements, such as medians, altitudes, and diagonals, will also be congruent between the congruent triangles.
- Hence, we have successfully proven CPCTC, which states that corresponding parts of congruent triangles are congruent.
The proof of CPCTC relies on the foundation of triangle congruence, which can be established through different congruence criteria.
Once the congruence of the triangles is established, the proof applies the congruence relationships to the corresponding parts of the triangles, including sides, angles, and other elements.
Properties
The property of Corresponding Parts of Congruent Triangles are Congruent (CPCTC) states that if two triangles are congruent, their corresponding parts (sides, angles, and other elements) are also congruent. Let’s explore the properties of CPCTC in detail:
Corresponding Sides
When two triangles are congruent, CPCTC ensures their corresponding sides are congruent. This means that the lengths or measures of the sides in one triangle are equal to the lengths or measures of the corresponding sides in the other triangle. For example, if triangle ABC is congruent to triangle DEF, then AB = DE, BC = EF, and AC = DF.
Corresponding Angles
CPCTC also guarantees that the corresponding angles of congruent triangles are congruent. This implies that the angles in one triangle are equal to the measures of the corresponding angles in the other triangle. For instance, if triangle ABC is congruent to triangle DEF, then ∠A = ∠D, ∠B = ∠E, and ∠C = ∠F.
Other Corresponding Elements
CPCTC extends beyond sides and angles to include other corresponding elements of congruent triangles. These elements include medians, altitudes, diagonals, and other geometric properties. If two triangles are congruent, CPCTC ensures that their corresponding elements, such as medians AB’ and DE’ or altitudes CD and FG, are also congruent.
Application in Geometric Reasoning
CPCTC is crucial in geometric reasoning and proof construction. By establishing the congruence of triangles using methods such as SAS, SSS, or ASA, CPCTC allows for applying congruence relationships to individual parts of triangles. This aids in proving various geometric theorems and solving problems involving congruent triangles.
Construction of Congruent Figures
CPCTC enables the construction of congruent figures using known congruent triangles. By knowing that corresponding parts of congruent triangles are congruent, we can create figures or shapes with specific congruence relationships based on the congruence of their component triangles.
Generalizability
The property of CPCTC is not limited to triangles but can be extended to other polygons. If two polygons are congruent, their corresponding parts will also be congruent, following the principles of CPCTC.
CPCTC is a powerful property in geometry that ensures that corresponding parts of congruent triangles (or polygons) are congruent. This property provides a reliable foundation for geometric reasoning, proof construction, and the exploration of congruence relationships among various elements of geometric figures.
Historical Significance
The historical background of the principle “Corresponding Parts of Congruent Triangles are Congruent” (CPCTC) traces back to the development of Euclidean geometry and the study of triangles.
Euclidean geometry, named after the ancient Greek mathematician Euclid, formed the foundation of geometric reasoning and proof construction. Euclid’s work, particularly his seminal work “Elements,” established a rigorous axiomatic system for geometry and introduced various theorems and principles.
The concept of congruent triangles, where two triangles have the same shape and size, dates back to ancient times. However, the specific idea that corresponding parts of congruent triangles are congruent is attributed to the work of Euclid and his followers.
Euclid’s “Elements” (circa 300 BCE) served as a comprehensive compilation of the mathematical knowledge of the time. Book I of “Elements” focused on plane geometry, including studying triangles and their properties.
Within Book I, Euclid introduced the concept of congruence and the criteria for triangle congruence, such as Side-Angle-Side (SAS), Side-Side-Side (SSS), and Angle-Side-Angle (ASA). These criteria provided a basis for proving that the two triangles were congruent.
While Euclid did not explicitly state the CPCTC principle as a separate theorem, it was implicit in his work. Euclid’s theorems and proofs demonstrated the congruence of corresponding parts by relying on the established criteria for triangle congruence.
Over time, as Euclidean geometry became widely studied and disseminated, the principle of CPCTC gained recognition as a powerful tool for establishing congruence relationships between corresponding parts of triangles.
Throughout history, mathematicians and geometers built upon Euclid’s work and expanded the field of geometry. Theorems and principles related to congruent triangles, including CPCTC, were refined, extended, and applied in various mathematical contexts.
Today, CPCTC is a fundamental principle in geometric reasoning and proof construction. It continues to be taught and utilized in geometry curricula worldwide, serving as a key concept for establishing congruence relationships and making deductions about the corresponding parts of congruent triangles.
The historical background of CPCTC showcases its development alongside the broader evolution of geometry, from Euclid’s foundational work to modern applications and advancements. The principle has endured over centuries, offering mathematicians and students a powerful tool for exploring the geometric properties of triangles.
Applications
The principle of Corresponding Parts of Congruent Triangles is Congruent (CPCTC) finds applications in various fields where geometry is fundamental. Here are some notable applications of CPCTC:
Geometric Proofs
CPCTC is a fundamental tool in geometric proofs, allowing mathematicians to establish congruence relationships between corresponding parts of triangles. It enables the construction of logical and rigorous arguments to prove geometric theorems, establish relationships between figures, and deduce properties based on congruence.
Engineering and Architecture
CPCTC is applied in engineering and architecture to ensure accuracy and consistency in the design and construction of structures. By utilizing congruent triangles, engineers and architects can ensure that corresponding parts of structural components, such as beams, trusses, or supports, are identical in size and shape, enhancing stability and structural integrity.
Surveying and Mapping
CPCTC plays a vital role in surveying and mapping applications. It allows surveyors to establish congruence between corresponding points, angles, or sides on the ground and in maps or plans. This aids in accurately measuring, positioning, and mapping land boundaries, infrastructure, and geographic features.
Computer-Aided Design (CAD)
CPCTC is utilized in CAD software to ensure consistency and precision in geometric modeling and design. By applying CPCTC principles, CAD systems can automatically maintain congruence relationships between corresponding parts of objects, facilitating accurate transformations, scaling, and assembly of components in virtual design environments.
Robotics and Kinematics
CPCTC ensures precise movements and alignments of robotic limbs or end effectors in robotics. By establishing congruence between corresponding parts of robotic components, engineers can achieve accurate positioning and kinematic control, enabling tasks such as pick-and-place operations, assembly, and robotic manipulations.
Physics and Trigonometry
CPCTC finds applications in physics and trigonometry, where the congruence of triangles is utilized to analyze geometric properties and physical phenomena. Using CPCTC, physicists can establish congruence between corresponding parts of triangles in various contexts, such as projectile motion, wave propagation, or electrical circuit analysis.
Navigation and Global Positioning Systems (GPS)
CPCTC establishes congruence between corresponding elements in navigation systems and GPS technology in triangulation methods. By ensuring congruence between measured angles or distances, GPS systems can accurately determine positions on Earth’s surface and aid in navigation and tracking applications.
Art and Design
CPCTC is utilized in art and design to create visually pleasing and harmonious compositions. Artists and designers often apply the principles of CPCTC to establish congruent relationships between corresponding elements in their works, such as shapes, forms, or patterns, ensuring balance and visual coherence.
The applications of CPCTC extend beyond these examples and find relevance in various fields where geometric reasoning, congruence, and consistency play a crucial role. CPCTC enables accurate measurements, reliable proofs, and precise geometric relationships, enhancing the understanding and application of geometry in practical contexts.
Exercise
Example 1
Triangle ABC is congruent to triangle DEF. Prove: Angle ABC is congruent to angle DEF.
Solution
Since triangle ABC is congruent to triangle DEF, we can write it as:
∠A ≅ ∠D
∠B ≅ ∠E
∠C ≅ ∠F
Therefore, by CPCTC, we can conclude that angle ABC is congruent to angle DEF.
Example 2
Triangle PQR is congruent to triangle STU. Prove: Side PQ is congruent to side ST.
Solution
Since triangle PQR is congruent to triangle STU, we can write it as:
PQ ≅ ST
QR ≅ TU
PR ≅ SU
By CPCTC, we can conclude that side PQ is congruent to side ST.
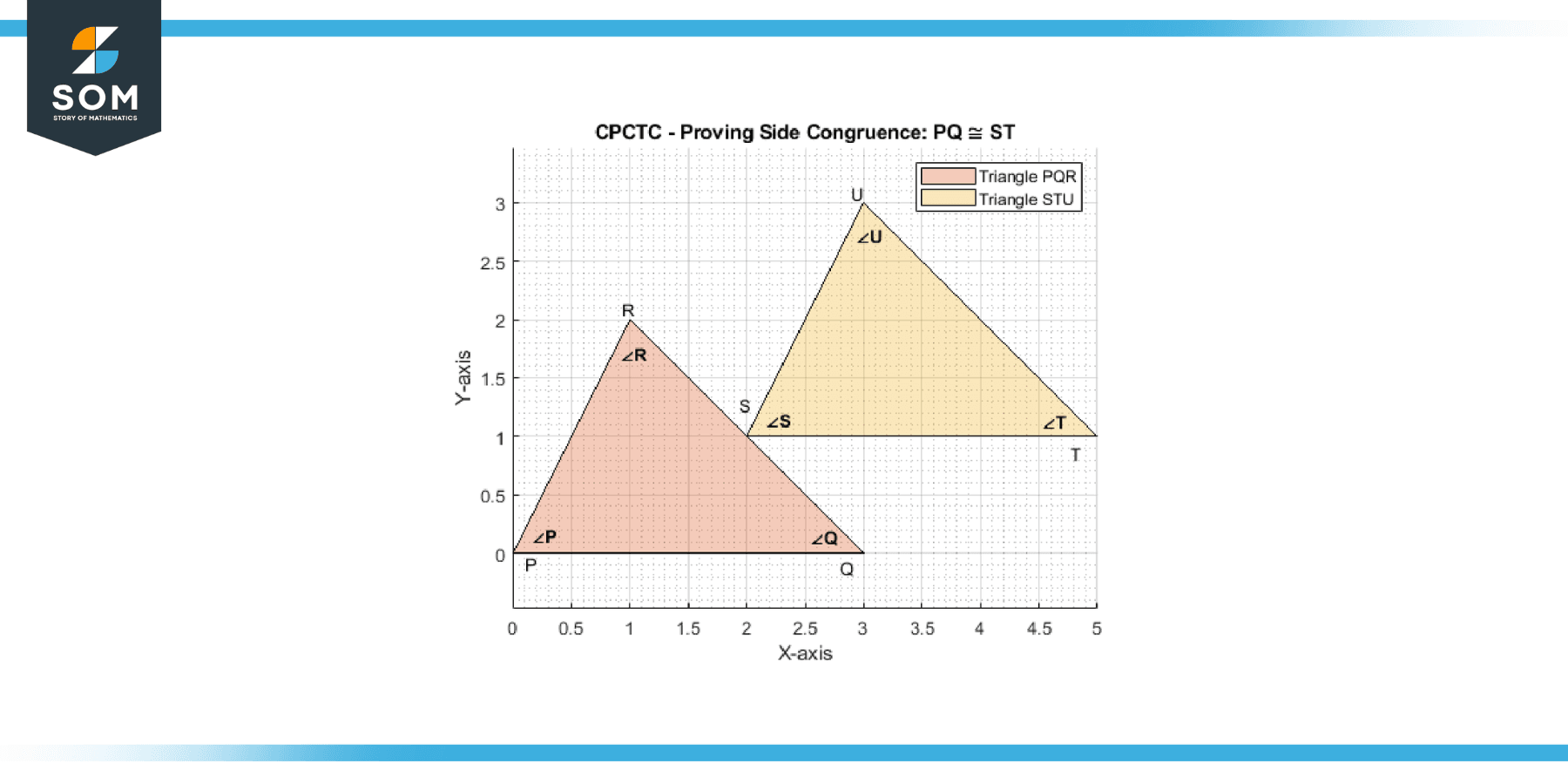
Figure-2.
Example 3
Triangle XYZ is congruent to triangle UVW. Prove: Side XY is congruent to side VW.
Solution
Since triangle XYZ is congruent to triangle UVW, we can write it as:
XY ≅ UV
XZ ≅ UW
YZ ≅ VW
By CPCTC, we can conclude that side XY is congruent to side VW.
Example 4
Triangle MNO is congruent to triangle PQR. Prove: Angle M is congruent to angle P.
Solution
Since triangle MNO is congruent to triangle PQR, we can write it as:
∠M ≅ ∠P
∠N ≅ ∠Q
∠O ≅ ∠R
By CPCTC, we can conclude that angle. M is congruent to angle P.
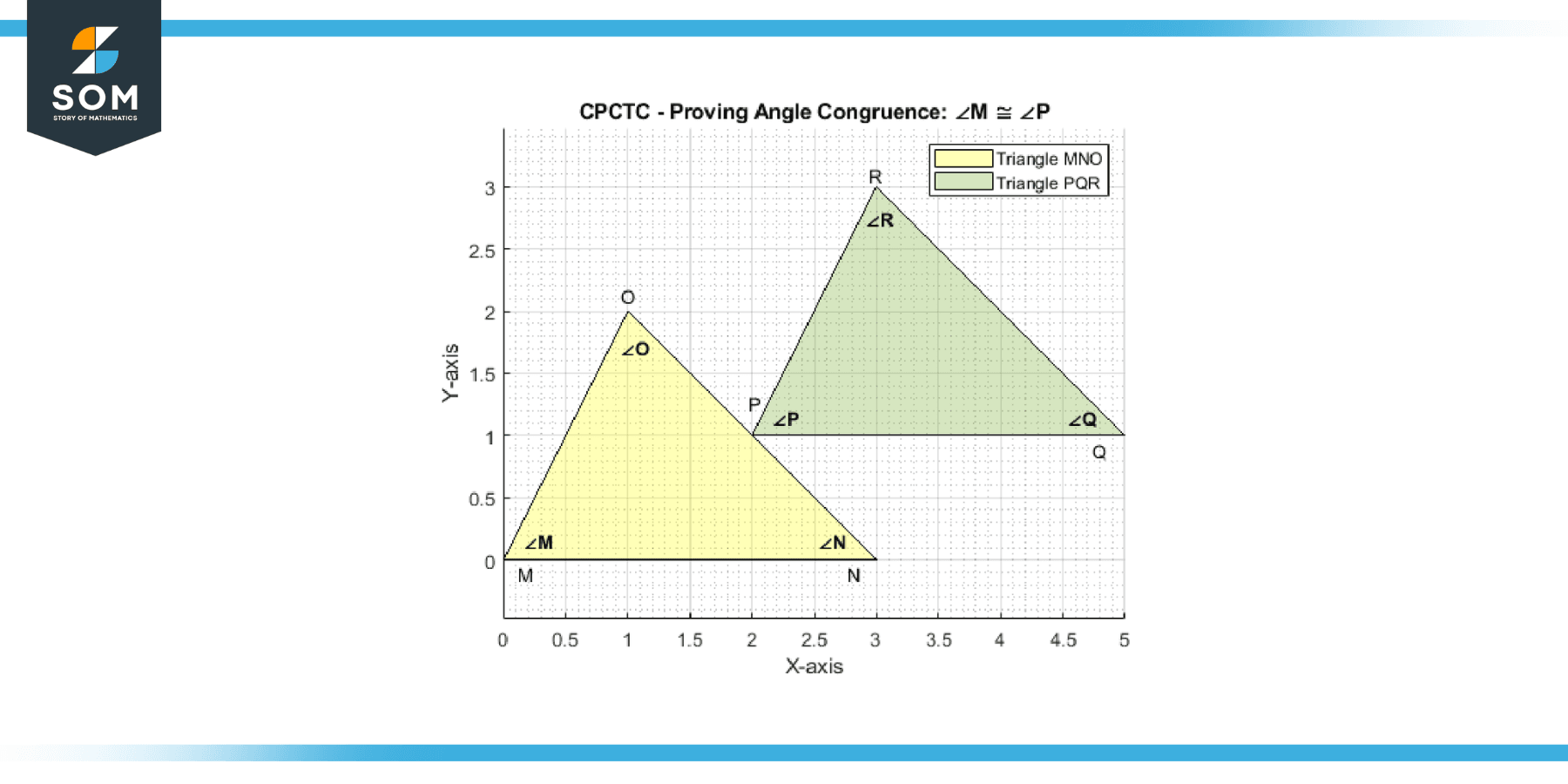
Figure-3.
Example 5
Triangle DEF is congruent to triangle GHI. Prove: Side DE is congruent to side GH.
Solution
Since triangle DEF is congruent to triangle GHI, we can write it as:
DE ≅ GH
EF ≅ HI
DF ≅ GI
By CPCTC, we can conclude that side DE is congruent to side GH.
Example 6
Triangle JKL is congruent to triangle MNP. Prove: Angle K is congruent to angle N.
Solution
Since triangle JKL is congruent to triangle MNP, we can write it as:
∠K ≅ ∠N
∠J ≅ ∠M
∠L ≅ ∠P
By CPCTC, we can conclude that angle K is congruent to angle N.
Example 7
Triangle ABC is congruent to triangle XYZ. Prove: Side AC is congruent to side XZ.
Solution
Since triangle ABC is congruent to triangle XYZ, we can write it as:
AC ≅ XZ
AB ≅ XY
BC ≅ YZ
By CPCTC, we can conclude that side AC is congruent to side XZ.
Example 8
Triangle RST is congruent to triangle UVW. Prove: Angle S is congruent to angle U.
Solution
Since triangle RST is congruent to triangle UVW, we can write it as:
∠S ≅ ∠U
∠R ≅ ∠V
∠T ≅ ∠W
By CPCTC, we can conclude that angle S is congruent to angle U.
All images were created with MATLAB.
