- Home
- >
- Construct an Angle Bisector – Explanation & Examples
JUMP TO TOPIC
Construct an Angle Bisector – Explanation and Examples
 Given an angle ABC, it is possible to construct a line BF that divides the angle into two equal parts using only a straightedge and compass. Such a line is called an angle bisector.
Given an angle ABC, it is possible to construct a line BF that divides the angle into two equal parts using only a straightedge and compass. Such a line is called an angle bisector.
Constructing an angle bisector requires that we construct an isosceles triangle BDE inside the angle and then construct an equilateral triangle DEF that shares a base with BDE. If we then construct the line BF, it will divide the original angle ABC into two equal angles.
Doing this requires that we have a thorough understanding of the basics of construction. It is also a good idea to review the equilateral triangles’ construction, covered in the construction of a 60-degree angle.
This topic will go over:
- How to Construct an Angle Bisector
- How to Construct an Angle Bisector with Compass
- Proof that the Angles are Equal
How to Construct an Angle Bisector
Suppose we are given an angle ABC. It can be acute, right, or obtuse. It doesn’t matter.
We want to construct an angle bisector. That is, we want to construct a new line that will divide the angle into two equal angles.
To do this, we will need our straightedge, compass, and a few of Euclid’s theorems. Specifically, we need to know that if two triangles have all three sides congruent, then the triangles are congruent. This means that their corresponding angles will be equal.
How to Construct an Angle Bisector with Compass
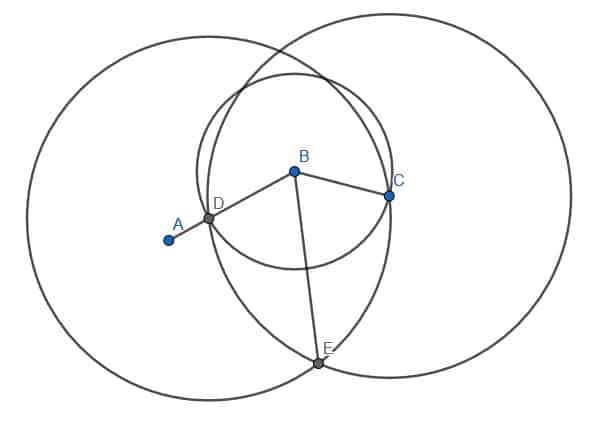
First, we pick a point D on AB.
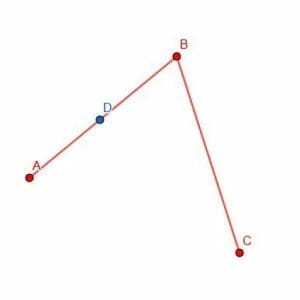
Next, we can place the point of the compass at B and the pencil tip at D. Then, we can trace out the circumference of a circle with center B and radius BD. Mark the place where this circle intersects BC as E.
Note that in practice, it’s sufficient to create an arc from D to E instead of creating the whole circle. Since the whole circle is necessary for the proof, however, we will construct it here.
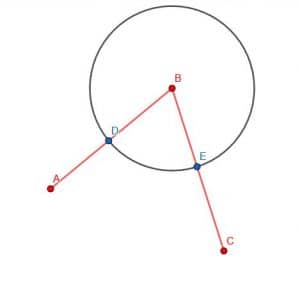
Next, we will connect D and E using our straightedge. Then, we will construct an equilateral triangle with DE as an edge. Recall that we do this by creating two circles with radius DE. One will be centered at D, while the other will be centered at E. We will call the intersection F and construct the lines DF and EF. We want this triangle to point away from B, as shown.
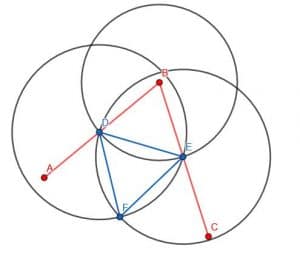
Finally, we can connect points B and F with our straightedge. The line BF will create two angles, ABF and FBC, that are equal to each other.
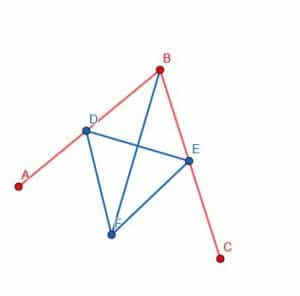
Examples
In this section, we will go over common problems that involve the construction of an angle bisector.
Example 1
Prove that BF bisects the angle ABC.
Example 1 Solution
Let’s consider the construction again.

The line segment BD equals the line segment BE because they are both radii of the circle with center B and radius BD. We also know that the line segment DF is equal to the line segment EF because they are both legs of an equilateral triangle. Of course, the line segment BF is equal to itself in length.
Thus, the legs of the triangles DBF and EBF are the same. Consequently, the two triangles are congruent. This means that their corresponding angles are congruent. Specifically, the angles ABF and CBF are equal. Since these two angles together make up the original angle, ABC, the line BF bisects ABC.
Example 2
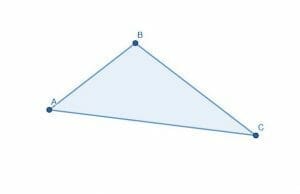
Divide the triangle in two using an angle bisector. Are the two parts equal in area?
Example 2 Solution
We’ll divide the angle ABC as before. Rather than constructing a new point D, we can use the endpoint of the shorter side, A.
Then, we draw a circle with center B and radius BA and label the intersection of this circle with the line BC as D.
Then, we create two circles with radius AD. One will have center A, and the other will have center D. If we draw a line from B to the intersection of these two circles, E, we have an angle bisector as shown.
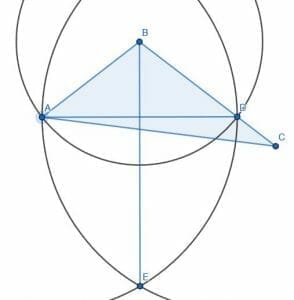
The two triangles, in this case, will not be equal. Let’s call the intersection of AD and BE F. ABF and EBF are congruent because AB and BD were constructed to be radii of the circle with center B and radius AB. BF is, of course, equal to itself, and we have already shown that the angles ABF and CBF are equal. Therefore, the two triangles ABF and DBF are congruent by Elements 1.4, which states that two triangles are congruent if two sides are the same and the angle between them is the same.
If we call the intersection of the lines AC and BE G and connect CG, we can see that the triangle AFG is equal to CFG. However, there is still an additional area remaining to the right of BE. Consequently, the triangle has not been cut in half even though the angle ABC has been bisected.
Example 3
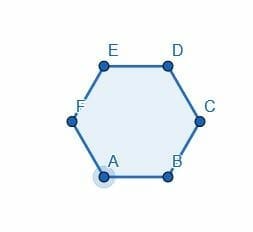
Divide the hexagon into two halves using an angle bisector.
Example 3 Solution
When we constructed 60-degree angles, we showed that a hexagon is actually composed of 6 equilateral triangles. Therefore, if we cut this in half, we should be able to put 3 equilateral triangles in each half.
In this case, we can use any angle. We’ll use the angle ABC to be consistent, though. A and C are already equidistant from B because this is a regular hexagon. This, we can connect them with a line and construct an equilateral triangle ACG. Then, we connect B and G to bisect the angle ABC.
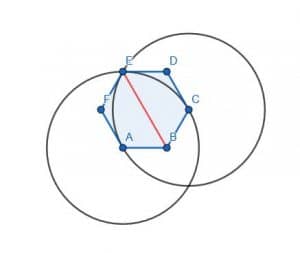
Note, however, that G and E are the same point. This makes sense because A and C are separated by one angle, but so are the pair A and E and the pair C and E.
Thus, bisecting the angle ABC does bisect the hexagon.
Example 4
Divide the angle into four equal parts.
Example 4 Solution
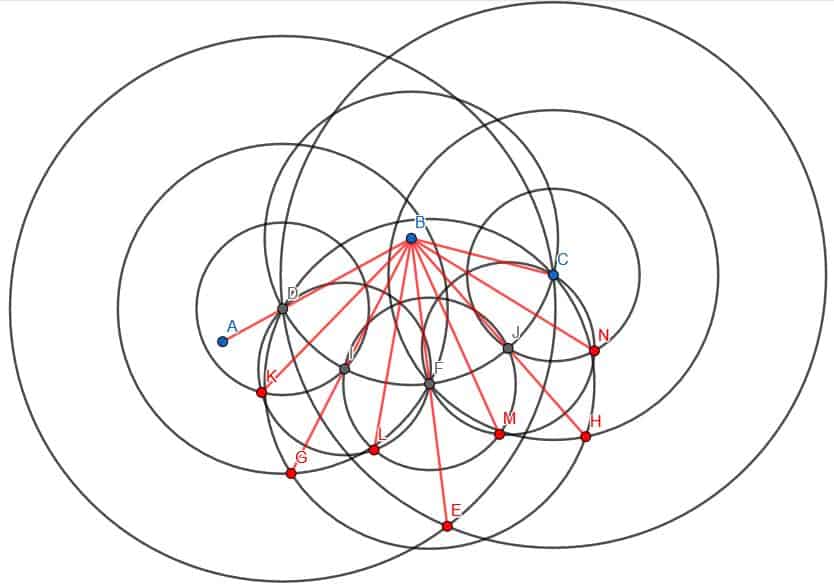
When we divide an angle in two, we double the number of angles. Therefore, to divide an angle in four, we must first bisect the angle. Then, we must bisect the two new angles formed.
We’ll bisect the angle as before. In this case, we can use the shorter side’s endpoint, C, as the radius of the circle centered at B. We’ll call the intersection of this circle with the line AB D. We can then create two new circles with radius CD, one centered at C and one at D. We’ll call the intersection E and connect BE. So far, we’ve just bisected the angle.
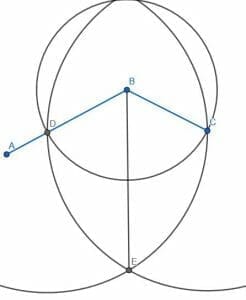
Now we need to bisect the angles ABE and CBE.
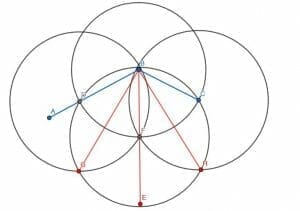
We can call the intersection of the circle centered at B with radius BC and the line BE F. Then, we can create three new circles. They will each have radius FD, which will be equal to FC, and there will be one centered at D, one centered at F, and one centered at C.
If we construct a line from B to the intersection of the circles centered at D and F with radius FD, we will bisect ABF. Likewise, if we construct a line from B to the intersection of the circles centered at C and F with radius FC, we will bisect CBF. Since ABF and CBF were equal in measure, their bisected angles will also be equal in measure.
Thus, we have cut the original angle ABC into four equal parts.
Example 5
Divide the angle greater than a straight line into two equal parts.
Example 5 Solution
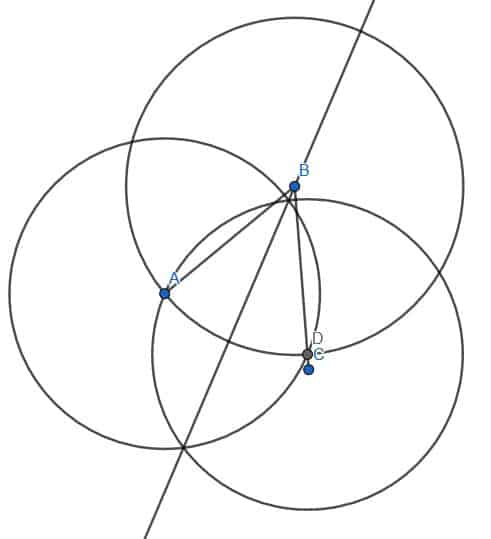
The greater angle here is the one measured clockwise as ABC. We can try using the same tactics as before. This is because when we bisect the smaller angle measured counterclockwise as ABC, we can bisect the larger angle by extending the angle bisector.
Let’s do this. First, we bisect the acute angle ABC as before, finding a point on BC equal in length to BA. We’ll call this point D. Then, we construct two circles of length AD, one centered at A and one at D. Drawing a line from B to this intersection, E, gives us an angle bisector. We can then extend the line through the circle we constructed to find the point D.
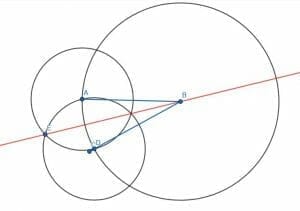
Since this line goes through the center of the circle and touches the circumference in both directions, it is the diameter of the circle with center B and radius BA. We can see that the larger angle ABC has been cut into two parts. If we look, one part is a straight line minus ABE, and the other is a straight line minus DBE. Since ABE=DBE, the two angles that the larger angle ABC has been cut into are equal.
Practice Questions
![]()
Open Problems
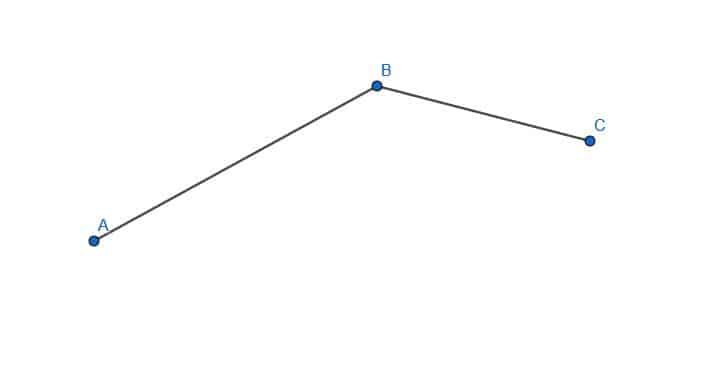
- Bisect the given angle.

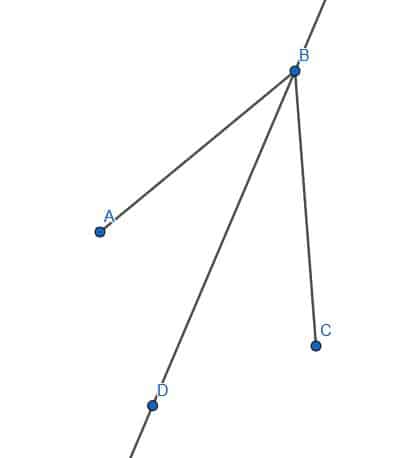
- Cut the given angle into 8 equal parts.

- Does the line CD bisect the angle ACB?

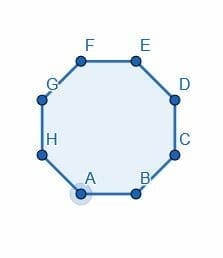
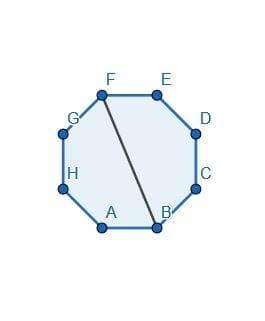
- Divide the octagon in half by bisecting one of the angles.

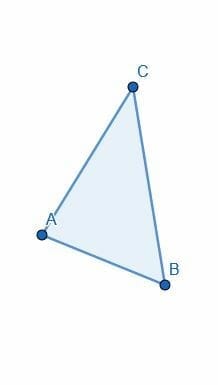
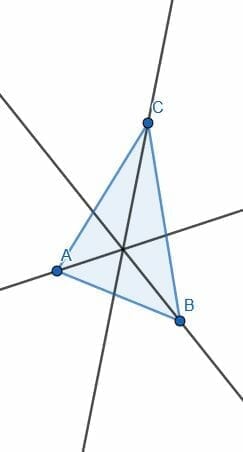
- Bisect each of the angles of the triangle given.

Open Problem Solutions
Yes, because it lines up with a constructed bisector.
4. 
5.
Images/mathematical drawings are created with GeoGebra.