JUMP TO TOPIC
Construction of a 30 Degree Angle – Explanation and Examples
 Constructing a 30-degree angle with a straightedge and compass requires constructing a 60-degree angle and an angle bisector.
Constructing a 30-degree angle with a straightedge and compass requires constructing a 60-degree angle and an angle bisector.
Since an equilateral triangle has three 60 degree angles, we need to construct an angle from an equilateral triangle and then divide it into two halves with an angle bisector. Note that axiomatic geometry does not include measurements, so technically, we are constructing an angle that is one-sixth of a straight line or one-third of a right angle.
Since this construction relies heavily on constructing a 60-degree angle and constructing an angle bisector, make sure to review those sections before reading on.
In this topic, we will go over:
- How to Construct a 30 Degree Angle
- How to Construct a 30 Degree Angle with Compass
- How to Construct a 30 Degree Angle with Ruler
How to Construct a 30 Degree Angle
Constructing a 30-degree angle requires us first to construct an equilateral triangle. Each of the angles in the triangle will have 60 degrees. Then, we can cut these angles in half with an angle bisector. The resulting angles will each be 30 degrees.
How to Construct a 30 Degree Angle with Compass
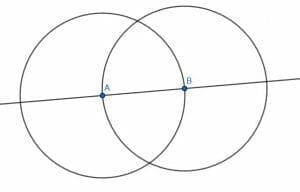
Suppose we are given a line segment AB, to begin with. Then, we can construct an equilateral triangle with AB as one of the sides. We’ll do this using our compass.
First, put the compass on A and the pencil point on B. Then, draw a circle by pivoting around the point A. Then, do the same with a circle centered at B with radius BA.
These two circles will intersect in two places.
How to Construct a 30 Degree Angle with Ruler
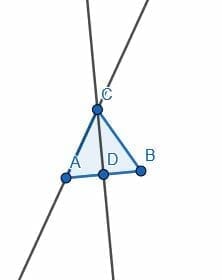
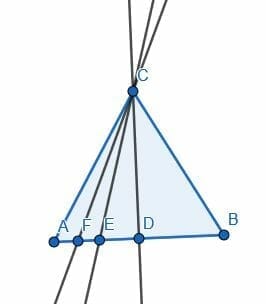
Then, we can use our ruler or straightedge to finish the construction. We can connect A to the upper point of intersection, which we will call C. We can then connect C to the lower point of intersection, D. ACD will be a 30-degree angle.
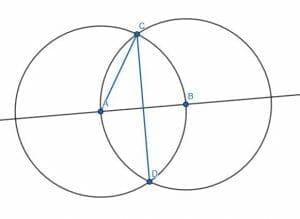
How do we know this is 30 degrees?
If we connect B to C, then the triangle ABC is equilateral. Likewise, if we connect AD and BD, ABD is equilateral. Therefore, the angle ACB is 60 degrees. This also means that connect CD will bisect the angle ACB. Therefore, ACD must be at a 30-degree angle.
Examples
Example 1
Construct a right angle using 30-degree angles.
Example 1 Solution
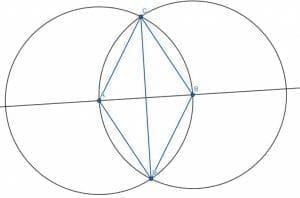
We begin with a line segment AB.

Next, we create the equilateral triangle ABC by constructing two circles with length AB. One will have center A, and the other will have center B. Their intersection will be C.
Then, we bisect the angle C by constructing another equilateral triangle on AB, ABD, and connecting C and D.
The angles ACD, BCD, BDC, and ADC will all be 30-degree angles because they are all half of a 60-degree angle.
Example 2
Construct a 150-degree angle.
Example 2 Solution
We’ll begin by constructing a straight line, AB. This line will have an angle of 180 degrees.
We know that a 150-degree angle is five-sixths of a straight line. That is, if we construct one 30-degree line on the straight line, we’ll have two angles—one of 30 degrees and one of 150 degrees.
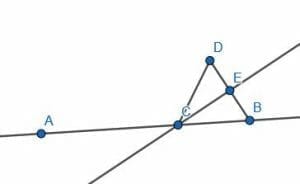
Let’s start with a line AB.

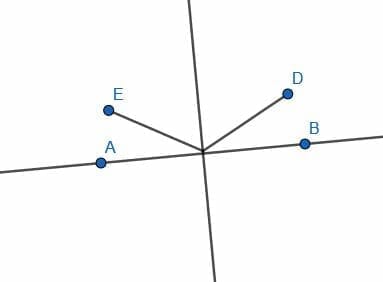
Pick a random point C on AB. Then, construct an equilateral triangle BCD on the segment BC.
Next, we can bisect the angle DCB and label the intersection with DB as E.
The angle ACB is the straight line, so it has a measure of 180 degrees. The angle ECB has a measure of 30 degrees. Therefore, the remainder, angle ACE, has a measure of 150 degrees.
Example 3
Construct a 15-degree angle.
Example 3 Solution
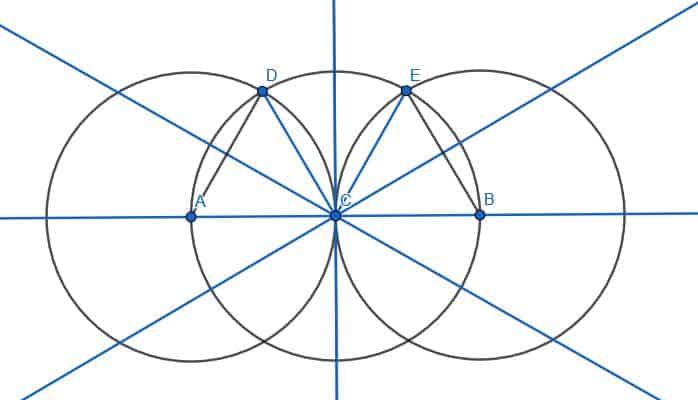
A 15-degree angle is half of a 30-degree angle. Thus, we can construct such an angle by first creating an equilateral triangle. We can then divide one of the angles into four equal parts by bisecting it and then bisecting the two new angles. Then, each of the four resulting angles will be 15 degrees.
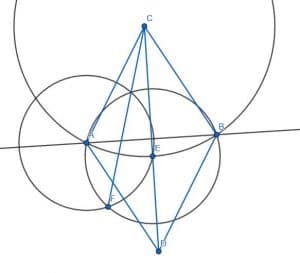
We begin with a line AB.

Then, we construct two equilateral triangles, ABC and ABD, on AB as in example 1. If we connect C and D, we will have constructed two 30 degree angles, ACD and BCD.

We can then divide the angle ACD into two parts by first creating a circle with center C and radius CA. We can then label the intersection of CD and this circle as E. If we create two more circles with radius AE, one with center A and one with center E, we can label the intersection F and connect CF. ACF and ECF are both 15-degree angles because CF bisects the 30-degree angle ACE.
Example 4
Construct a 75-degree angle.
Example 4 Solution
In this case, we need to add a 15-degree angle, like the one constructed in example 3, onto a 60-degree angle.
We begin by constructing an equilateral triangle ABC.
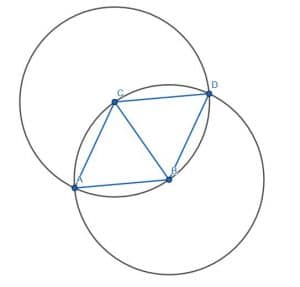
Then, we construct another equilateral triangle next to it by creating a circle with center C and radius CB. We label the place where this circle intersects the circle with center B and radius BA as D. Then, we construct the triangle CDB.
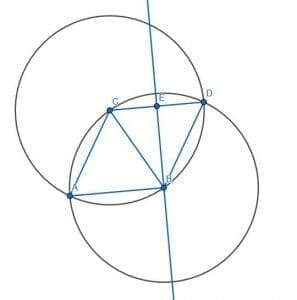
Now, we need to divide the angle CBD into two equal halves with an angle bisector. Then, label the point where this line intersects CD as E. This will create the 30-degree angle CBE.
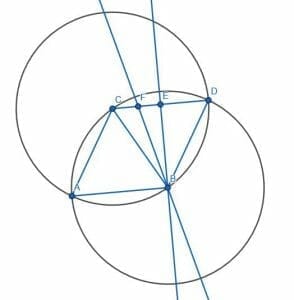
Finally, we can bisect the angle CBE and label the intersection of this line and CE as F. Thus, the angle CBF will be 15 degrees. Since ABC is 60 degrees, ABF is 75 degrees, as required.
Example 5
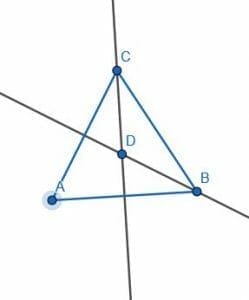
Construct an isosceles triangle with two 30 degree angles.
Example 5 Solution
Once again, we will begin with an equilateral triangle.

This time, we will bisect the angles ACB and CBA. We can label the intersection as D.
CDB is then an isosceles triangle because DCB and DBC are equal angles. Since these angles are each half of the original angles, each is 30 degrees. Therefore, CDB is the required triangle.
Practice Questions
![]()
Open Problems
- Construct a 30-degree angle on the given line.

- Construct a 30-degree angle, a 120-degree angle, and a 30-degree angle on the given line.

- Construct a $7.5$-degree angle.
- Show that six $30$ degree angles fit on a straight line.
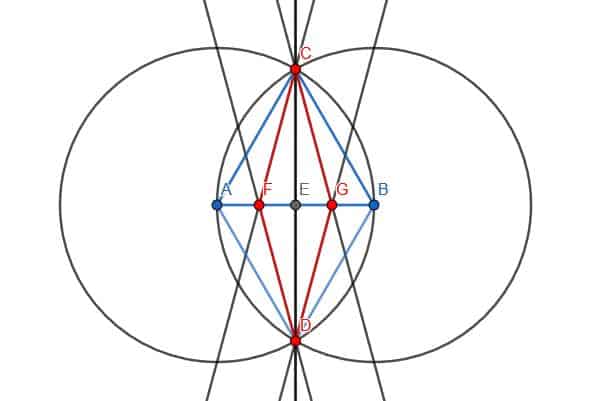
- Construct a rhombus with one set of angles equal to $30$ degrees.
Open Problem Solutions
The red quadrilateral is a rhombus with a 30-degree angle pair.
Images/mathematical drawings are created with GeoGebra.