JUMP TO TOPIC
Congruent supplementary angles are angles that meet two conditions — they are congruent and they are supplementary. These angles share these properties, making them unique angles and important ones to learn when working with applications and problems involving angles and algebra.
Congruent supplementary angles are angles that add up to $\boldsymbol{180^{\circ}}$ and, at the same time, share the same angle measure. These angles will always have angle measures of $\boldsymbol{90^{\circ}}$.
This article covers different examples of congruent supplementary angles and establishes the reason why their angle measures are always $90^{\circ}$. Expect examples and practice questions near the end of the discussion to test your understanding of congruent supplementary angles.
What Are Congruent Supplementary Angles?
Congruent supplementary angles are angles that have angle measures of $90^{\circ}$ each. The pair of angles must have equal angle measures and at the same time, add up to $180^{\circ}$, hence the name of the angle. This means that there are no other congruent supplementary angles other than the pair of right angles.
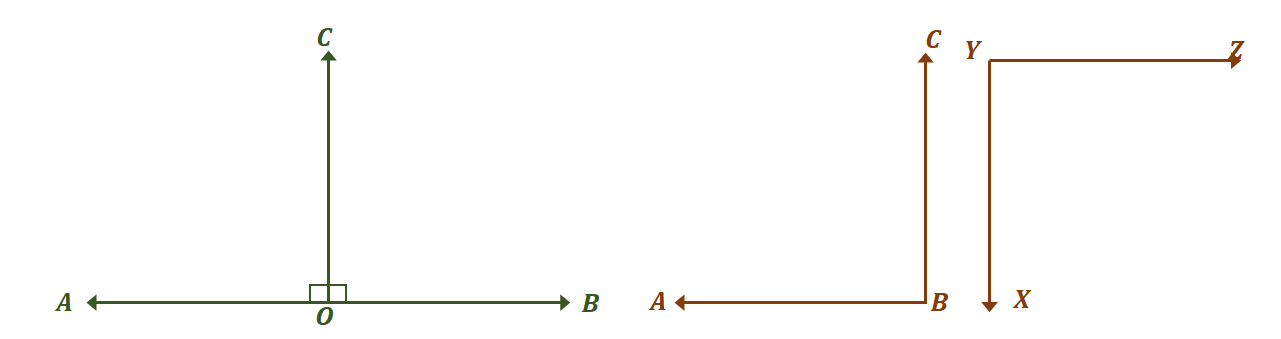
Take a look at the two pairs of angles shown above and see how they are both pairs of congruent supplementary angles. First, focus on the linear pair of angles and find the measures of the angle that make them congruent.
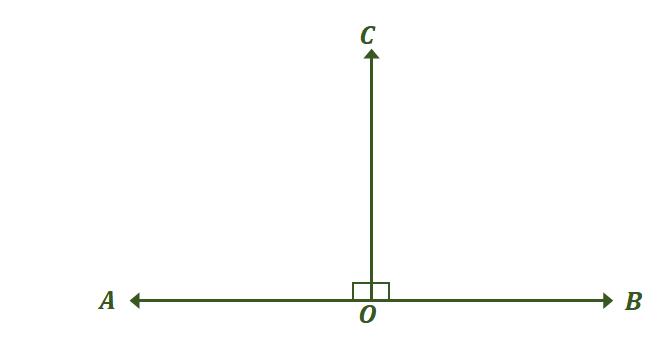
The two angles, $\angle AOC$ and $\angle BOC$, are linear pairs, so they form a linear angle and add up to $180^{\circ}$. For the two angles to be congruent, $\angle AOC = \angle BOC = 90^{\circ}$.
This means that the only time that a linear pair of angles (consequently, a pair of supplementary angles) are congruent to each other is when they are both right angles. This is consistent with what was established about congruent supplementary angles.
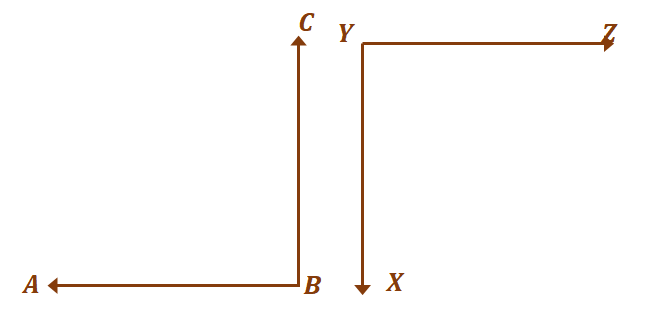
Let’s move on to the second pair of angles, $\angle ABC$ and $XYZ$. As discussed in the past, supplementary angles don’t have to form other angles.
As long as they add up to $180^{\circ}$, the two angles are considered supplementary. Now, for the two angles to be congruent and at the same time supplementary, $\angle ABC = \angle XYZ = 90^{\circ}$.
The two examples highlight the fact that the only possible pair of angles that are congruent and supplementary are two right angles. Of course, it’s important to understand the reasoning behind this and generalize the rule for all situations.
How To Prove Congruent Supplementary Angles?
To prove congruent supplementary angles, use the definition of congruent angles and supplementary angles then find the angle measures that can only satisfy the two conditions. For example, suppose that the two angles, $\angle M$ and $\angle N$, are two congruent angles. Meaning, their angle measures are equal.
\begin{aligned}\angle M &= \angle N\end{aligned}
If the two angles are also supplementary, $\angle M$ and $\angle N$’s angle measures add up to $180^{\circ}$.
\begin{aligned}\angle M + \angle N &= 180^{\circ} \end{aligned}
Substitute $\angle M = \angle N$ into the equation to find the measures of $\angle M$ and $\angle N$.
\begin{aligned}\angle N + \angle N &= 180^{\circ} \\2\angle N &= 180^{\circ}\\ \angle N &= 90^{\circ}\end{aligned}
Since $\angle M$ and $\angle N$ are congruent, $\angle M = \angle N = 90^{\circ}$. This proves that for two angles to be congruent supplementary angles, their angle measures must be two right angles or must measure $90^{\circ}$ each.
Using Congruent Supplementary Angles
Use the congruent supplementary angles and their measures to solve different problems involving angles. When the angles are labeled as both congruent and supplementary, there is no need to solve for their measures since it’s already established that they’re both right angles.
When solving for unknown values given two congruent supplementary angles, simply equate each expression representing the congruent supplementary angles to $90^{\circ}$. Use this when solving the sample problem shown below.
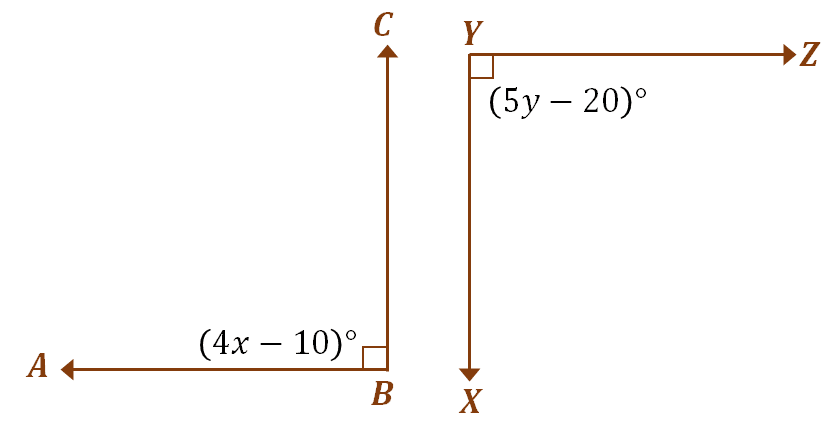
Suppose that $\angle ABC$ and $\angle XYZ$ are congruent supplementary angles, use the previous discussion to find the values of $x$ and $y$. Since the two angles are congruent supplementary, they each measure $90^{\circ}$. To find the values of $x$ and $y$, equate each angle’s expression to $90^{\circ}$.
\begin{aligned}\boldsymbol{\angle ABC}\end{aligned} | \begin{aligned}\boldsymbol{\angle XYZ}\end{aligned} |
\begin{aligned}\angle ABC &= 90^{\circ}\\(4x – 10)^{\circ} &= 90^{\circ}\\4x&= 100\\x &= 25\end{aligned} | \begin{aligned}\angle XYZ &= 90^{\circ}\\(5y – 20)^{\circ} &= 90^{\circ}\\ 5y&= 110\\y &= 22\end{aligned} |
Hence, using the definition of congruent supplementary angles, $x = 25$ and $y = 22$. Apply a similar process when working with congruent supplementary angles, and when you’re ready, head over to the section below to try out more problems!
Example 1
The lines $l_1$ and $l_2$ are two intersecting lines that are also perpendicular to each other. They form four angles: $\angle 1$, $\angle 2$, $\angle 3$, and $\angle 4$. Confirm $\angle 1 \,\&\, \angle 2$ and $\angle 3 \,\&\, \angle 4$ are congruent supplementary angles.
Solution
When working with problems like this, it’s helpful to construct the diagram. Sketch a pair of intersecting lines that are perpendicular to each other as well. This means that these two lines form four $L$-shaped quadrants similar to a rectangular coordinate system.
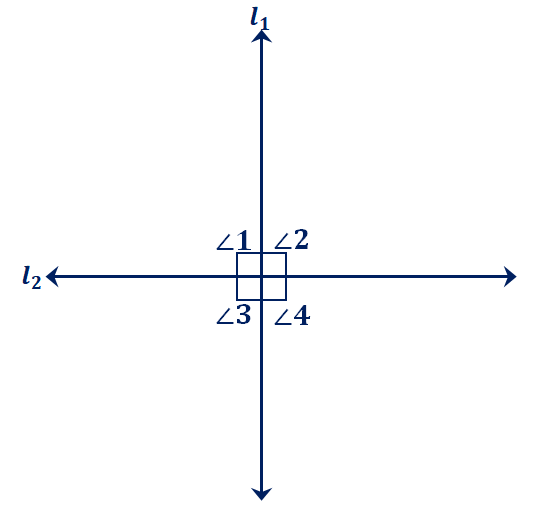
Observe the upper half of the section, which are the quadrants containing $\angle 1$ and $\angle 2$. These angles form a line, so they add up to $180^{\circ}$. Since it has been established that $l_1$ and $l_2$ are perpendicular to each other, $\angle 1$ and $\angle 2$ are right angles. This means that they each measure $90^{\circ}$.
\begin{aligned}\angle 1 &= \angle 2\\&= 90^{\circ}\end{aligned}
The same explanation applies for the lower section, which is $\angle 3 = \angle 4 = 90^{\circ}$. Of course, each pair of angles will add up to $180^{\circ}$. This also means that by rearranging the angles, the result will remain the same.
\begin{aligned}\angle 1 &= \angle 3\\&= 90^{\circ}\end{aligned} | \begin{aligned}\angle 2 &= \angle 4\\&= 90^{\circ}\end{aligned} |
\begin{aligned}\angle 1 &= \angle 4\\&= 90^{\circ}\end{aligned} | \begin{aligned}\angle 2 &= \angle 3\\&= 90^{\circ}\end{aligned} |
Example 2
\begin{aligned}\angle A &= (6x – 30)^{\circ}\\\angle B &= (4y – 30)^{\circ}\end{aligned}
The angles $\angle A$ and $\angle B$ are congruent supplementary angles, so what are the values of $x$ and $y$?
Solution
Recall that when two angles are congruent supplementary angles, they both measure $90^{\circ}$. This means that the two angles, $\angle A$ and $\angle B$, measure $90^{\circ}$.
Find the values of $x$ and $y$ by equating the expressions for $\angle A$ and $\angle B$ to $90^{\circ}$ each.
\begin{aligned}\boldsymbol{\angle ABC}\end{aligned} | \begin{aligned}\boldsymbol{\angle XYZ}\end{aligned} |
\begin{aligned}\angle ABC &= 90^{\circ}\\(6x – 30)^{\circ} &= 90^{\circ}\\6x&= 120\\x &= 20\end{aligned} | \begin{aligned}\angle XYZ &= 90^{\circ}\\(4y – 30)^{\circ} &= 90^{\circ}\\ 4y&= 120\\y &= 30\end{aligned} |
Example 3
Angles $\angle AOC$ and $\angle BOC$ are perpendicular to each other and form a line. If $\angle AOC = (5x – 10)^{\circ}$ and $\angle BOC = (4y – 70)^{\circ}$, what is the value of $x + y$?
Solution
Construct an image describing the problem — it should look similar to our earlier example of linear pair that are also supplementary angles as shown below. Label the appropriate angles and include their angle measures.
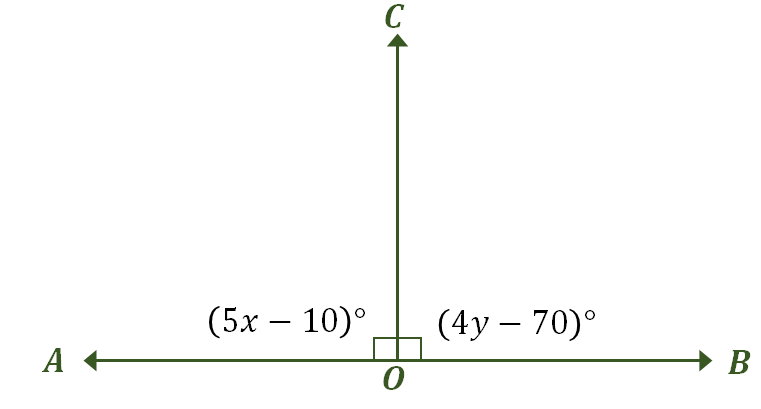
In the first part of this discussion, it has been established that when a linear pair has angles that are congruent measures, the only possible measure of both angles is $90^{\circ}$. In fact, these are also congruent supplementary angles, so the fastest way to solve this problem is by equating $\angle AOC$ and $BOC$’s expressions to $90^{\circ}$.
\begin{aligned}\boldsymbol{\angle AOC}\end{aligned} | \begin{aligned}\boldsymbol{\angle BOC}\end{aligned} |
\begin{aligned}\angle AOC &= 90^{\circ}\\(5x – 10)^{\circ} &= 90^{\circ}\\5x &= 130\\x &= 26\end{aligned} | \begin{aligned}\angle BOC &= 90^{\circ}\\(4y – 70)^{\circ} &= 90^{\circ}\\ 4y&= 160\\y &= 40\end{aligned} |
This means that $x = 26$ and $y = 40$, so using these results, $x + y = 66$.
These three problems highlight how much easier it is to solve similar problems once the measure of congruent supplementary angles are established. When you’re ready to try out more practice questions, head over to the section below!
Practice Questions
1. True or False: All supplementary angles are congruent.
2. True or False: All linear pair are congruent supplementary angles.
3. True or False: Perpendicular lines will always form congruent supplementary angles.
4. Using the diagram shown below, which of the following statements is not true?

A. The angles, $\angle 1$ and $\angle 2$, are congruent supplementary angles.
B. The angles, $\angle 1$ and $\angle 3$, are perpendicular to each other.
C. The angles, $\angle 1$ and $\angle 4$, are perpendicular to each other.
D. The angles, $\angle 3$ and $\angle 4$, are congruent supplementary angles.
5. Suppose that $\angle LOM$ and $\angle MON$ are two congruent supplementary angles. If $x = 20$ and $y = 30$, which of the following expressions for $\angle LOM$ and $\angle MON$ are not valid?
A. $\angle LOM = (3x + 60)^{\circ}$, $\angle MON = (5y + 10)^{\circ}$
B. $\angle LOM = (5x – 10)^{\circ}$, $\angle MON = (2y + 30)^{\circ}$
C. $\angle LOM = (4x + 10)^{\circ}$, $\angle MON = (3y)^{\circ}$
D. $\angle LOM = (6x – 30)^{\circ}$, $\angle MON = (4y – 30)^{\circ}$
6. Angles $\angle AOC$ and $\angle BOC$ are perpendicular to each other and form a line. If $\angle AOC = (2x + 40)^{\circ}$ and $\angle BOC = (3y + 60)^{\circ}$, what is the value of $x + y$?
A. $x + y = 25$
B. $x + y = 35$
C. $x + y = 45$
D. $x + y = 55$
Answer Key
1. False
2. False
3. True
4. C
5. A
6. B
