Chords of a Circle – Explanation & Examples

In this article, you’ll learn:

• What a chord of a circle is.
• Properties of a chord and; and
• How to find the length of a chord using different formulas.

What is the Chord of a Circle?

By definition, a chord is a straight line joining 2 points on the circumference of a circle. The diameter of a circle is considered to be the longest chord because it joins to points on the circumference of a circle.

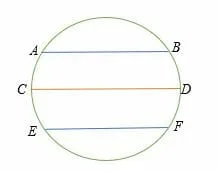
In the circle below, AB, CD, and EF are the chords of the circle. Chord CD is the diameter of the circle.

Properties of a Chord

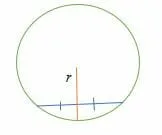
• The radius of a circle is the perpendicular bisector of a chord.

• The length of a chord increases as the perpendicular distance from the center of the circle to the chord decreases and vice versa.
• The diameter is the longest chord of a circle, whereby the perpendicular distance from the center of the circle to the chord is zero.
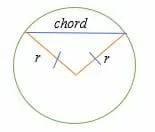
• Two radii joining the ends of a chord to the center of a circle form an isosceles triangle.

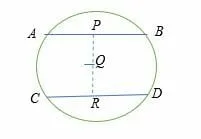
• Two chords are equal in length if they are equidistant from the center of a circle. For example, chord AB is equal to chord CD if PQ = QR.

How to Find the Chord of a Circle?

There are two formulas to find the length of a chord. Each formula is used depending on the information provided.

• The length of a chord, given the radius and distance to the center of a circle.

If the length of the radius and distance between the center and chord is known, then the formula to find the length of the chord is given by,

Length of chord = 2√ (r² – d²)

Where r = the radius of a circle and d = the perpendicular distance from the center of a circle to the chord.

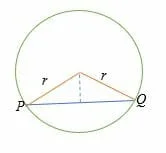
In the above illustration, the length of chord PQ = 2√ (r² – d²)

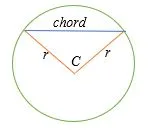
• The length of a chord, given the radius and central angle

If the radius and central angle of a chord are known, then the length of a chord is given by,

Length of a chord = 2 × r × sine (C/2)

= 2r sine (C/2)

Where r = the radius of the circle

C = the angle subtended at the center by the chord

d = the perpendicular distance from the center of a circle to the chord.

Let’s work out a few examples involving the chord of a circle.

Example 1

The radius of a circle is 14 cm, and the perpendicular distance from the chord to the center is 8 cm. Find the length of the chord.

Solution

Given radius, r = 14 cm and perpendicular distance, d = 8 cm,

By the formula, Length of chord = 2√(r²−d²)

Substitute.

Length of chord = 2√ (14²−8²)

= 2√ (196 − 64)

= 2√ (132)

= 2 x 11.5

= 23

So, the length of the chord is 23 cm.

Example 2

The perpendicular distance from the center of a circle to the chord is 8 m. Calculate the chord’s length if the circle’s diameter is 34 m.

Solution

Given the distance, d = 8 m.

Diameter, D = 34 m. So, radius, r = D/2 = 34/2 = 17 m

Length of chord = 2√(r²−d²)

By substitution,

Length of chord = 2√ (17² − 8²)

= 2√ (289 – 64)

= 2√ (225)

= 2 x 15

= 30

So, the length of the chord is 30 m.

Example 3

The length of a chord of a circle is 40 inches. Suppose the perpendicular distance from the center to the chord is 15 inches. What is the radius of the chord?

Solution

Given, length of chord = 40 inches.

Distance, d = 15 inches

Radius, r =?

By the formula, Length of chord = 2√(r²−d²)

40 = 2√ (r² − 15²)

40 = 2√ (r² − 225)

Square both sides

1600 = 4 (r² – 225)

1600 = 4r² – 900

Add 900 on both sides.

2500 = 4r²

Dividing both sides by 4, we get,

r² = 625

√r² = √625

r = -25 or 25

Length can never be a negative number, so we pick positive 25 only.

Therefore, the radius of the circle is 25 inches.

Example 4

Given that radius of the circle shown below is 10 yards and the length of PQ is 16 yards. Calculate the distance OM.

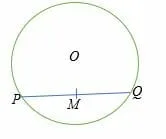
Solution

PQ = length of chord = 16 yards.

Radius, r = 10 yards.

OM = distance, d =?

Length of chord = 2√(r²−d²)

16 =2√ (10 ²− d ²)

16 =2√ (100 − d ²)

Square both sides.

256 = 4(100 − d ²)

256 = 400 − 4d²

Subtract 400 on both sides.

-144 = − 4d²

Divide both sides by -4.

36 = d²

d = -6 or 6.

Thus, the perpendicular distance is 6 yards.

Example 5:

Calculate the length of the chord PQ in the circle shown below.

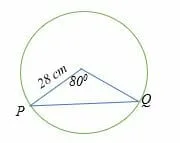
Solution

Given the central angle, C = 80⁰

The radius of the circle, r = 28 cm

Length of chord PQ =?

By the formula, length of chord = 2r sine (C/2)

Substitute.

Length of chord = 2r sine (C/2)

= 2 x 28 x Sine (80/2)

= 56 x sine 40

= 56 x 0.6428

= 36

Therefore, the length of the chord PQ is 36 cm.

Example 6

Calculate the length of the chord and the central angle of the chord in the circle shown below.

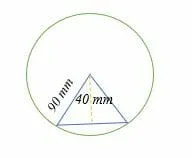
Solution

Given,

Perpendicular distance, d = 40 mm.

Radius, r = 90 mm.

Length of chord = 2√(r²−d²)

= 2√ (90² − 40²)

= 2 √ (8100 − 1600)

= 2√6500

= 2 x 80.6

= 161.2

So, the length of the chord is 161.2 mm

Now calculate the angle subtended by the chord.

Length of chord = 2r sine (C/2)

161.2 = 2 x 90 sine (C/2)

161.2 = 180 sine (C/2)

Divide both sides by 180.

0.8956 = sine (C/2)

Find the sine inverse of 0.8956.

C/2 = 63.6 degrees

Multiply both sides by 2

C = 127.2 degrees.

So, the central angle subtended by the chord is 127.2 degrees.