Area of a Parallelogram – Explanation & Examples

As the name suggests, a parallelogram is a quadrilateral formed by two pairs of parallel lines. It differs from a rectangle in terms of the measure of angles at the corners. In a parallelogram, the opposite sides are equal in length, and opposite angles are equal in measure, while in a rectangle, all angles are 90 degrees.

In this article, you will learn how to calculate the area of a parallelogram using the parallelogram area formula.

To find how its area is different from other quadrilaterals and polygons, visit the previous articles.

How to Find the Area of a Parallelogram?

The area of a parallelogram is the space enclosed by 2 pairs of parallel lines.  A rectangle and a parallelogram have similar properties, and therefore, the area of a parallelogram is equal to the area of a rectangle.

Area of a Parallelogram Formula

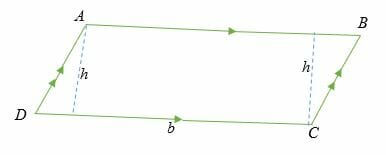
Consider a parallelogram ABCD shown below. The area of the parallelogram is the space bounded by the sides AD, DC, CB, and AB.

The area of parallelogram formula states;

Area of a parallelogram = base x height

A = (b * h) Sq. units

Where b = the base of a parallelogram and,

h = The altitude or the height of a parallelogram.

The height or altitude is the perpendicular line (usually dotted) from the vertex of a parallelogram to any of the bases.

Example 1

Calculate the area of a parallelogram whose base is 10 centimeters and height is 8 centimeters.

Solution

A = (b * h) Sq. units.

A = (10 * 8)

A = 80 cm²

Example 2

Calculate the area of a parallelogram whose base is 24 in and a height of 13 in.

Solution

A = (b * h) Sq. units.

= (24 * 13) square inch.

= 312 square inches.

Example 3

If the base of a parallelogram is 4 times the height and the area is 676 cm², find the parallelogram’s base and height.

Solution

Let the height of the parallelogram = x

and the base = 4x

But, the area of a parallelogram = b * h

676 cm² = (4x * x) Sq. units

676 = 4x²

Divide both sides by 4 to get,

169 = x²

By finding the square root of both sides, we get,

x = 13.

Substitute.

Base = 4 * 13 = 52 cm

Height = 13 cm.

Therefore, the base and height of the parallelogram are 52 cm and 13 cm, respectively.

Apart from the area of the parallelogram formula, there are other formulas for calculating the area of a parallelogram.

Let’s take a look.

How to find the area of a parallelogram without a height?

If the parallelogram’s height is unknown to us, we can use the trigonometry concept to find its area.

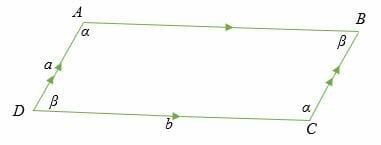
Area = ab sine (α) =ab sine (β)

Where a and b are the length of parallel sides, and either β or α is the angle between the sides of the parallelogram.

Example 4

Find the area of a parallelogram if its two parallel sides are 80 cm and 40 cm and the angle between them is 56 degrees.

Solution

Let a = 80 cm and b = 40 cm.

The angle between a and b = 56 degrees.

Area = ab sine (α)

Substitute.

A = 80 × 40 sine (56)

A = 3,200 sine 56

A = 2,652.9 sq.cm.

Example 5

Calculate the angles between the two sides of a parallelogram if its side lengths are 5 m and 9 m and the area of the parallelogram is 42.8 m².

Solution

Area of a parallelogram = ab sine (α)

42.8 m² = 9 * 5 sine (α)

42.8 = 45 sine (α)

Divide both sides by 45.

0.95111= sin (α)

α = sine^-1 0.95111

α = 72°

But β + α = 180°

β = 180° – 72°

= 108°

Therefore, the angles between the two parallel sides of the parallelogram are; 108° and 72°.

Example 6

Calculate the height of a parallelogram whose parallel sides are 30 cm and 40 cm, and the angle between these two sides is 36 degrees. Take the base of the parallelogram to be 40 cm.

Solution

Area = ab sine (α) = bh

30 * 40 sine (36) = 40 * h

1,200 sine (36) = 40 * h.

Divide both sides by 40.

h = (1200/40) sine 36

= 30 sine 36

h = 17.63 cm

So, the height of the parallelogram is 17.63 cm.

How to find the area of a parallelogram using diagonals?

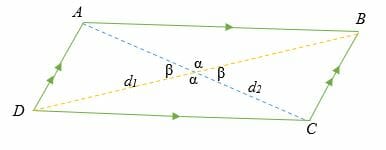
Suppose d₁ and d₂ are the diagonals of the parallelogram ABCD, then the area of the parallelogram is given as,

A = ½ × d₁ × d₂ sine (β) = ½ × d₁ × d₂ sine (α)

Where β or α is the angle of intersection of the diagonals d₁ and d₂.

Example 7

Calculate the area of a parallelogram whose diagonals are 18 cm and 15 cm, and the angle of intersection between the diagonals is 43°.

Solution

Let d₁ = 18 cm and d₂ = 15 cm.

β = 43°.

A = ½ × d₁ × d₂ sine (β)

= ½ × 18 × 15 sine (43°)

= 135sine 43°

= 92.07 cm²

Therefore, the area of the parallelogram is 92.07 cm².