JUMP TO TOPIC
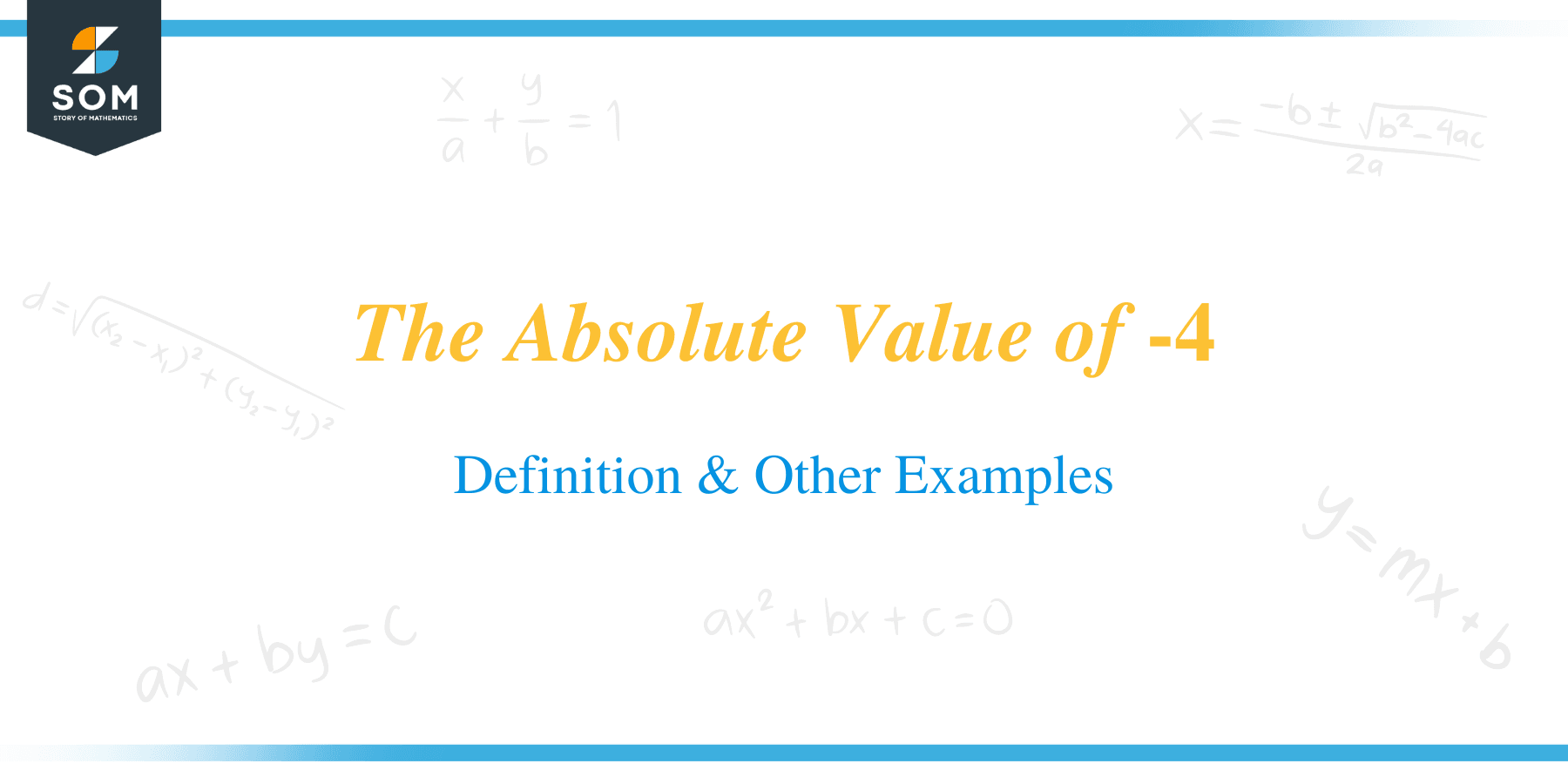 The absolute value of -4 is the positive, or more specifically, the nonnegative, real number $4$. The concept of absolute value has many applications in both mathematics and everyday life. Thus, learning how to solve for absolute values is important. In this article, we will discuss the definition of absolute value and how to find the absolute value of a number while also looking at some examples of absolute value in action.
The absolute value of -4 is the positive, or more specifically, the nonnegative, real number $4$. The concept of absolute value has many applications in both mathematics and everyday life. Thus, learning how to solve for absolute values is important. In this article, we will discuss the definition of absolute value and how to find the absolute value of a number while also looking at some examples of absolute value in action.
What Is the Absolute Value of -4?
The positive real number 4 is the absolute value of $-4$. In mathematics, the absolute value of a real number is the non-negative value without regard to its sign. For example, the absolute value of $3$ is $3$, and the absolute value of $−3$ is also $3$. The absolute value of a number is denoted by two vertical bars on either side of the number, as in $|\,|$. The absolute value of a number may also be thought of as its magnitude.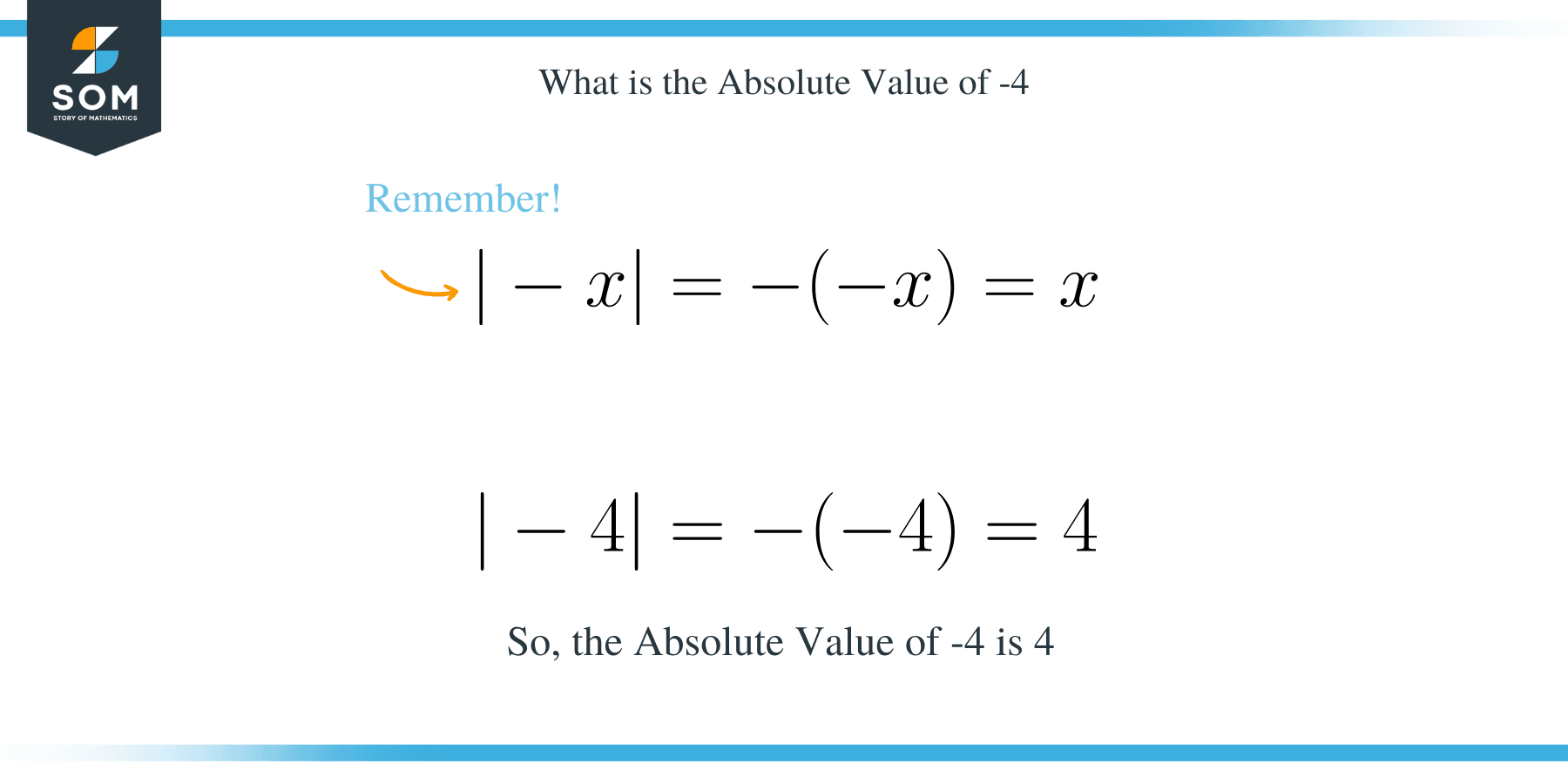
How Do You Find the Absolute Value of a Number?
The absolute value of a number is the numerical value of the number without any associated positive or negative sign. In other words, the absolute value of a number is the number’s distance from zero on a number line. If a number is negative, the absolute value of the number is the number with the negative sign removed. For example, the absolute value of $-5$ is $5$, and the absolute value of $5$ is also $5$. The absolute value of $0$ is $0$.
There are a few different ways to find the absolute value of a number. The most common way is to use the absolute value function on a graphing calculator. The function representing the absolute value is given by:
\begin{align*}
|x| = \left\{
\begin{array}{rcl}
x & \text{if } x\geq0\\
-x & \text{if }x<0
\end{array}\right.
\end{align*}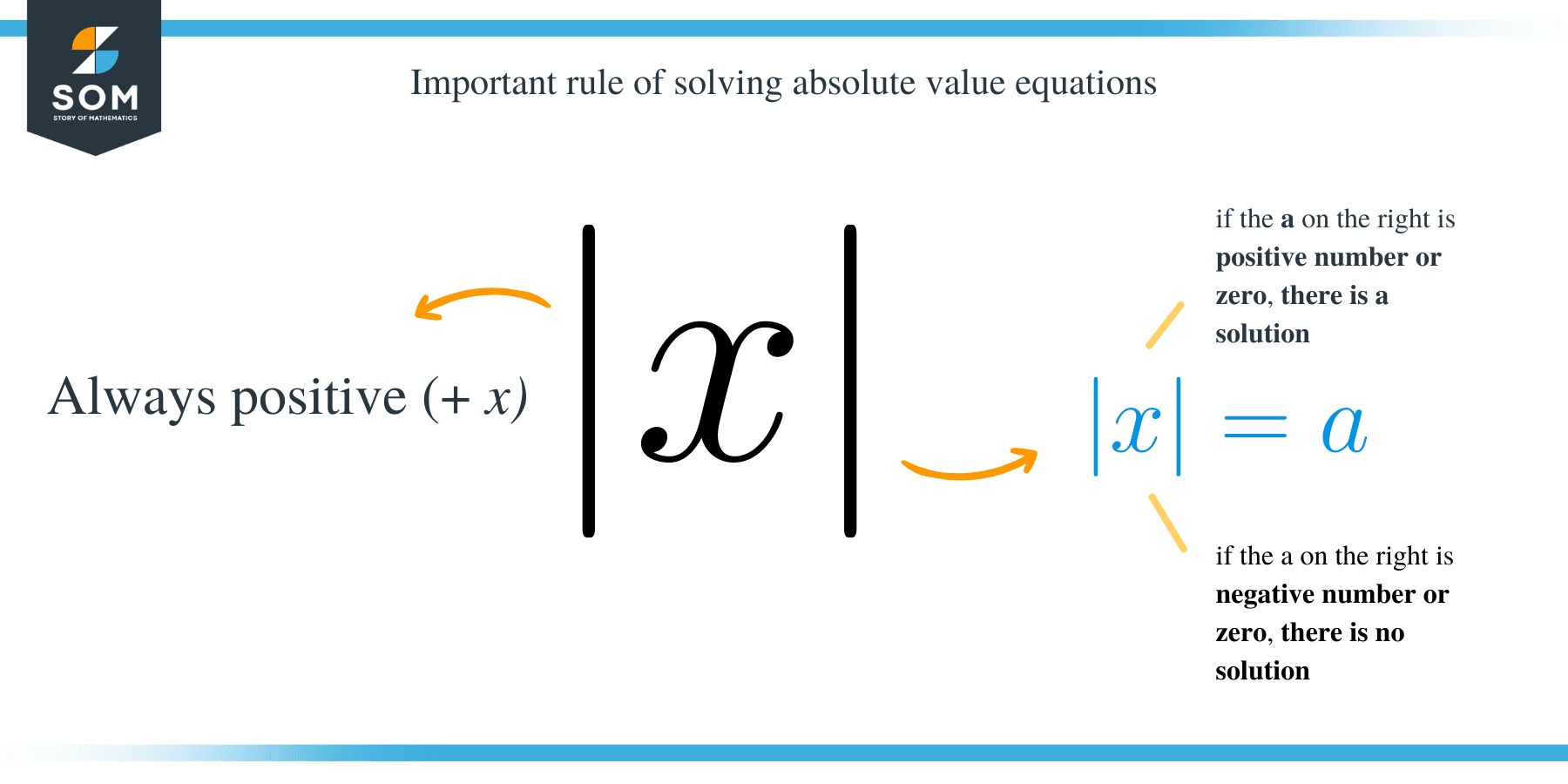
You can also use the properties of absolute values to solve equations and inequalities that involve absolute values. Keep reading to learn more about how to find the absolute value of a number from the following examples!
Example
- The absolute value of $-1$ is $1$. Since $-1$ is a negative number, then to get its absolute value, we just need to multiply it by negative $1$. That is:
\begin{align*}
|-1|=-(-1)=1.
\end{align*}
- The absolute value of $\dfrac{1}{2}$ is still $\dfrac{1}{2}$. We did not do anything to $\dfrac{1}{2}$ because it is a positive number.
- Zero is the absolute value of itself. Note that zero is neither negative nor positive. However, since it is not negative, then its absolute value is itself.
- The value of $|5-7|$ is $2$. This is obtained by performing the operation, first, inside the absolute value symbol, then determining the absolute of the resulting number after performing the operation. So, we have:
\begin{align*}
|5-7|=|-2|=2.
\end{align*}
Properties of the Absolute Value
- Nonnegativity: $|u|\geq0$ This means that the absolute value of a number is always greater than or equal to zero. This also means that it can never be positive.
- Positive-definiteness: $|u|=0$ if and only if $u=0$. The only time that the absolute value of a number is zero is whenever the number is zero.
- Symmetry: $|-u|=|u|$
- Multiplicativity: $|u\times v|=|u|\times|v|$
- Subadditivity: $|u+v|\leq|u|+|v|$
- Identity of indiscernible: $|u-v|=0$ if and only if $u=v$ This property is a consequence of positive-definiteness. Note that if $|u-v|$ is zero, then positive-definiteness guarantees that $u-v=0$. This implies that $u=v$. Moreover, if you start with the assumption that $u=v$, you will still arrive at the conclusion that $|u-v|=0$.
- Triangle inequality: $|u-v|\leq|u-w|+|w-v|$ The triangle inequality, on the other hand, is a property that resulted from the subadditivity property. Note that $u+v$ can also be written as $u-w+w-v$. So, we have: \begin{align*} |u-v|&=|(u-w+w-v)|\\ &=|(u-w)+(w-v)|. \end{align*} Applying subadditivity to the expression $|(u-w)+(w-v)|$, we have: \begin{align*} |(u-w)+(w-v)|\leq|u-w|+|w-v|. \end{align*} Thus, it follows that: \begin{align*} |u-v|\leq|u-w|+|w-v|. \end{align*}
- If y≠0, then $\left|\dfrac{x}{y}\right|=\dfrac{|x|}{|y|}$ .
- $|x-y|\geq\left||x|-|y|\right|$ This is also another consequence of subadditivity.
Example
We show how some of the properties work in the following examples.
- The symmetry property can be shown as |-7|=|7|=7.
- We show multiplicativity of the absolute value.
\begin{align*}
|2\times-4|=|-8|=8
\end{align*}
and
\begin{align*}
|2|\times|-4|=2\times4=8
\end{align*}
Thus, $|2\times-4|=|2|\times|-4|$.
- The preservation of division property is shown in this example.
\begin{align*}
\left|\dfrac{-4}{2}\right|=|-2|=2
\end{align*}
and
\begin{align*}
\dfrac{|-4|}{|2|} =\dfrac{4}{2}=2
\end{align*}
Then, $\left|\dfrac{-4}{2}\right|=\dfrac{|-4|}{|2|}$.
- Consider the following equations.
\begin{align*}
|2+(-4)|=|-2|=2
\end{align*}
and
\begin{align*}
|2|+|-4|=2+4=6.
\end{align*}
Note that $2<6$. Hence, $|2+(-4)|\leq|2|+|-4|$. Thus, the subadditivity property is satisfied.
- Note that $|7-10|=|-3|=3$. Say we take a real number $5$, then we have:
\begin{align*}
|7-5|+|5-10|&=|-2|+|-5|
&=2+5=7.
\end{align*}
We know that $3<7$, which means that $|7-10|\leq|7-5|+|5-10|$. Hence, the triangle inequality is satisfied.
- Consider the expressions $|8-(-3)|$ and $\left||8|-|-3|\right|$, and let’s establish their relationship. Note that \begin{align*} |8-(-3)|=|8+3|=|11|=11 \end{align*} and \begin{align*} |(|8|-|-3|=|8-3|)|=|5|=5 \end{align*} Moreover, note that $11>5$. This implies that
\begin{align*}
|8-(-3)|\geq\left||8|-|-3|\right|.
\end{align*}
Therefore, the last property of absolute value is satisfied in this example.
FAQ
What Is the Absolute Value of 2?
What Is the Answer to Finding the Absolute Value of -3?
How Do We Write the Absolute Value of -6?
What Is the Absolute Value of $ |-2|$?
The absolute value of $|-2|$ is $2$. Note that $|-2|$ is equal to $2$, and so the absolute value of $2$, which is already not a negative number, is also $2$.
Why Is the Absolute Value Can Never Be Negative?
Is Absolute Value Negative?
Conclusion
In conclusion, to find the absolute value of a number, you need to know the number’s distance from zero on a number line. This distance is always positive, so the absolute value of a number is always positive or zero. Aside from examples to show how to find the absolute value of a number, we also tackled some of the properties of absolute value that can be used to simplify mathematical expressions or show the relationship to other mathematical expressions involving absolute values.
- The absolute value of a number is the number itself whenever the number is positive or zero, and the number is multiplied by $-1$ if the number is negative.
- The absolute value of a number represents its magnitude without regard to its sign.
- The absolute value is either zero or a positive number and can never be negative.
- The absolute value of $-4$ is $4$.
With the knowledge of solving absolute values and applying their properties that we gather in this article, the discussion on absolute values can be further extended to two or more dimensional coordinate systems.
