45°-45°-90° Triangle – Explanation & Examples

Now that we know what a right triangle is and what the special right triangles are, it is time to discuss them individually. Let’s see what a 45°-45°-90° triangle is.

What is a 45°-45°-90° Triangle?

A 45°-45°-90° triangle is a special right triangle that has two 45-degree angles and one 90-degree angle. The side lengths of this triangle are in the ratio of;

Side 1: Side 2: Hypotenuse = n: n: n√2 = 1:1: √2.

The 45°-45°-90° right triangle is half of a square. This is because the square has each angle equal to 90°, and when it is cut diagonally, the one angle remains as 90°, and the other two 90° angles bisected (cut into half) and become 45° each.

The diagonal of a square becomes hypotenuse of a right triangle, and the other two sides of a square become the two sides (base and opposite) of a right triangle.

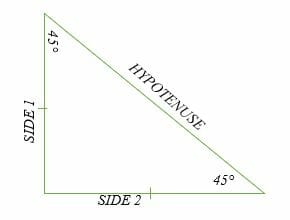
The 45°-45°-90° right triangle is sometimes referred to as an isosceles right triangle because it has two equal side lengths and two equal angles.

We can calculate the hypotenuse of the 45°-45°-90° right triangle as follows:

Let side 1 and side 2 of the isosceles right triangle be x.

Apply the Pythagorean Theorem a² + b² = c², where a and b are side 1 and 2 and c is the hypotenuse.

x² + x² = 2x²

Find the square root of each term in the equation

√x² + √x² = √(2x²)

x + x = x √2

Therefore, the hypotenuse of a 45°; 45°; 90° triangle is x √2

How to Solve a 45°-45°-90° Triangle?

Given the length of one side of a 45°-45°-90° triangle, you can easily calculate the other missing side lengths without resorting to the Pythagorean Theorem or trigonometric methods functions.

Calculations of a 45°-45°-90° right triangle fall into two possibilities:

• Case 1

To calculate the length of hypotenuse when given the length of one side, multiply the given length by √2.

• Case 2

When given the length of the hypotenuse of a 45°-45°-90° triangle, you can calculate the side lengths by simply dividing the hypotenuse by √2.

Note: Only the 45°-45°-90° triangles can be solved using the 1:1: √2 ratio method.

Example 1

The hypotenuse of a 45°; 45°; 90° triangle is 6√2 mm. Calculate the length of its base and height.

Solution

Ratio of a 45°; 45°; 90° triangle is n: n: n√2. So, we have;

⇒ n√2 = 6√2 mm

Square both sides of the equation.

⇒ (n√2)² = (6√2)² mm

⇒ 2n² = 36 * 2

⇒ 2n² = 72

n² = 36

Find the square root.

n = 6 mm

Hence, the base and height of the right triangle are 6 mm each.

Example 2

Calculate the right triangle’s side lengths, whose one angle is 45°, and the hypotenuse is 3√2 inches.

Solution

Given that one angle of the right triangle is 45 degrees, this must be a 45°-45°-90° right triangle.

Therefore, we use the n: n: n√2 ratios.

Hypotenuse = 3√2 inches = n√2;

Divide both sides of the equation by √2

n√2/√2 = 3√2/√2

n = 3

Hence, the length of each side of the triangle is 3 inches.

Example 3

The shorter side of an isosceles right triangle is 5√2/2 cm. What is the diagonal of the triangle?

Solution

An isosceles right triangle is the same as the 45°-45°-90° right triangle. So, we apply the ratio of n: n: n√2 to calculate the hypotenuse’s length.

Given that n = 5√2/2 cm;

⇒ n√2 = (5√2/2) √2

⇒ (5/2) √ (2 x 2)

⇒ (5/2) √ (4)

⇒ (5/2)2

= 5

Hence, the two legs of the triangle are 5 cm each.

Example 4

The diagonal of a 45°-45°-90°right triangle is 4 cm. What is the length of each of the legs?

Solution

Divide the hypotenuse by √2.

⇒ 4/√2

⇒ √4/√2

⇒ 4√2/2

= 2√2 cm.

Example 5

The diagonal of a square is 16 inches, calculate the length of the sides,

Solution

Divide the diagonal or hypotenuse by √2.

⇒ 16/√2

⇒ 16√2/√2 = 8√2

Hence, the length of the legs is 8√2 inches each.

Example 6

The angle of elevation of the top of a story building from a point on the ground 10 m from the base of the building is 45 degrees. What is the height of the building?

Solution

Given one angle as 45 degrees, assume a 45°- 45°-90°right triangle.

Apply the n: n: n√2 ratio where n = 10 m.

⇒ n√2 = 10√2

Therefore, the height of the building is 10√2 m.

Example 7

Find the length of the hypotenuse of a square whose side length is 12 cm.

Solution

To get the length of the hypotenuse, multiply the side length by √2.

⇒ 12 √2 = 10 √2

Hence, the diagonal is 10 √2 cm.

Example 8

Find the lengths of the other two sides of a square whose diagonal 4√2 inches.

Solution

A half of a square makes a 45°- 45°-90°right triangle. Therefore, we use the n: n: n√2 ratios.

n√2 = 4√2 inches.

divide both sides by √2

n = 4

Hence, the side lengths of the square are 4 inches each.

Example 9

Calculate the diagonal of a square flower garden whose side length is 30 m.

Solution

Apply the n: n: n√2 ratio, where n = 30.

⇒ n√2 = 30 √2

Therefore, the diagonal is equal to 30 √2 m