EUCLID OF ALEXANDRIA – The Father of Geometry

Euclid (c.330-275 BCE, fl. c.300 BCE)

Who is Euclid

The Greek mathematician Euclid lived and flourished in Alexandria in Egypt around 300 BCE, during the reign of Ptolemy I. Almost nothing is known of his life, and no likeness or first-hand description of his physical appearance has survived antiquity, and so depictions of him (with a long flowing beard and cloth cap) in works of art are necessarily the products of the artist’s imagination.

He probably studied for a time at Plato’s Academy in Athens but, by Euclid’s time, Alexandria, under the patronage of the Ptolemies and with its prestigious and comprehensive Library, had already become a worthy rival to the great Academy.

Euclid is often referred to as the “Father of Geometry”, and he wrote perhaps the most important and successful mathematical textbook of all time, the “Stoicheion” or “Elements”, which represents the culmination of the mathematical revolution which had taken place in Greece up to that time. He also wrote works on the division of geometrical figures into into parts in given ratios, on catoptrics (the mathematical theory of mirrors and reflection), and on spherical astronomy (the determination of the location of objects on the “celestial sphere”), as well as important texts on optics and music.

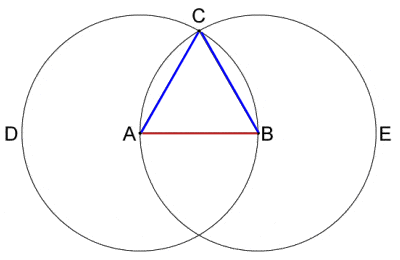Euclid’s method for constructing of an equilateral triangle from a given straight line segment AB using only a compass and straight edge was Proposition 1 in Book 1 of the “Elements”

The “Elements” was a lucid and comprehensive compilation and explanation of all the known mathematics of his time, including the work of Pythagoras, Hippocrates, Theudius, Theaetetus and Eudoxus. In all, it contains 465 theorems and proofs, described in a clear, logical and elegant style, and using only a compass and a straight edge. Euclid reworked the mathematical concepts of his predecessors into a consistent whole, later to become known as Euclidean geometry, which is still as valid today as it was 2,300 years ago, even in higher mathematics dealing with higher dimensional spaces. It was only with the work of Bolyai, Lobachevski and Riemann in the first half of the 19th Century that any kind of non-Euclidean geometry was even considered.

The “Elements” remained the definitive textbook on geometry and mathematics for well over two millennia, surviving the eclipse in classical learning in Europe during the Dark Ages through Arabic translations. It set, for all time, the model for mathematical argument, following logical deductions from inital assumptions (which Euclid called “axioms” and “postulates”) in order to establish proven theorems.

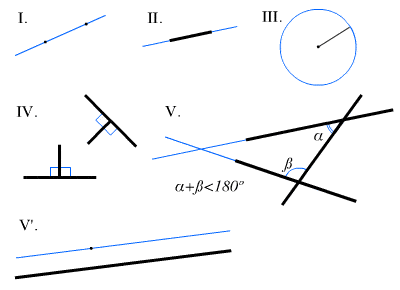
Euclid’s five general axioms were:

1. Things which are equal to the same thing are equal to each other.
2. If equals are added to equals, the wholes (sums) are equal.
3. If equals are subtracted from equals, the remainders (differences) are equal.
4. Things that coincide with one another are equal to one another.
5. The whole is greater than the part.

Euclid’s Postulates (1 – 5)

His five geometrical postulates were:

1. It is possible to draw a straight line from any point to any point.
2. It is possible to extend a finite straight line continuously in a straight line (i.e. a line segment can be extended past either of its endpoints to form an arbitrarily large line segment).
3. It is possible to create a circle with any center and distance (radius).
4. All right angles are equal to one another (i.e. “half” of a straight angle).
5. If a straight line crossing two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles.

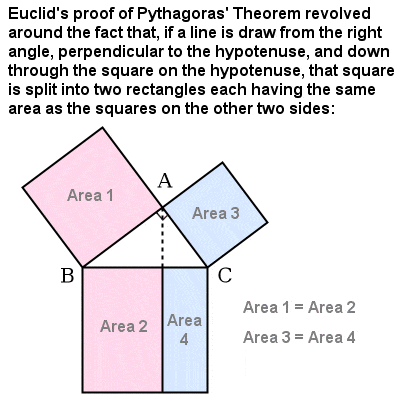Part of Euclid’s proof of Pythagoras’ Theorem

Among many other mathematical gems, the thirteen volumes of the “Elements” contain formulas for calculating the volumes of solids such as cones, pyramids and cylinders; proofs about geometric series, perfect numbers and primes; algorithms for finding the greatest common divisor and least common multiple of two numbers; a proof and generalization of Pythagoras’ Theorem, and proof that there are an infinite number of Pythagorean Triples; and a final definitive proof that there can be only five possible regular Platonic Solids.

However, the “Elements” also includes a series of theorems on the properties of numbers and integers, marking the first real beginnings of number theory. For example, Euclid proved what has become known as the Fundamental Theorem of Arithmethic (or the Unique Factorization Theorem), that every positive integer greater than 1 can be written as a product of prime numbers (or is itself a prime number). Thus, for example: 21 = 3 x 7; 113 = 1 x 113; 1,200 = 2 x 2 x 2 x 2 x 3 x 5 x 5; 6,936 = 2 x 2 x 2 x 3 x 17 x 17; etc. His proof was the first known example of a proof by contradiction (where any counter-example, which would otherwise prove an idea false, is shown to makes no logical sense itself).

He was the first to realize – and prove – that there are infinitely many prime numbers. The basis of his proof, often known as Euclid’s Theorem, is that, for any given (finite) set of primes, if you multiply all of them together and then add one, then a new prime has been added to the set (for example, 2 x 3 x 5 = 30, and 30 + 1 = 31, a prime number) a process which can be repeated indefinitely.

Euclid also identified the first four “perfect numbers”, numbers that are the sum of all their divisors (excluding the number itself):
6 = 1 + 2 + 3;
28 = 1 + 2 + 4 + 7 + 14;
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248; and
8,128 = 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1,016 + 2,032 + 4,064.
He noted that these numbers also have many other interesting properties. For example:

• They are triangular numbers, and therefore the sum of all the consecutive numbers up to their largest prime factor: 6 = 1 + 2 + 3; 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7; 496 = 1 + 2 + 3 + 4 + 5 + …. + 30 + 31; 8,128 = 1 + 2 + 3 + 4 + 5 + … + 126 + 127.
• Their largest prime factor is a power of 2 less one, and the number is always a product of this number and the previous power of two: 6 = 2¹(2² – 1); 28 = 2²(2³ – 1); 496 = 2⁴(2⁵ – 1); 8,128 = 2⁶(2⁷ – 1).

Although the Pythagoreans may have been aware of the Golden Ratio (φ, approximately equal to 1.618), Euclid was the first to define it in terms of ratios (AB:AC = AC:CB), and demonstrated its appearance within many geometric shapes.